Иловая теория каналов Кеннеди, ее концепция, ограничения и проектирование - Строительство и ремонт

Проектирование каналов с использованием теории ила Кеннеди объясняется в следующих разделах. Кроме того, будут представлены предположения относительно предложенной теории, ее концепции, ограничений и усовершенствований.

Процедура проектирования каналов с использованием теории ила Кеннеди

Пример 1
Пример 2

Что такое иловая теория Кеннеди?

Р.Г. Кеннеди исследовал системы каналов в течение двадцати лет и пришел к теории ила Кеннеди. Теория гласит, что ил, переносимый текущей водой в канале, удерживается во взвешенном состоянии вихревым течением, поднимающимся к поверхности.
Вертикальная составляющая вихревого течения стремится переместить осадок вверх, в то время как вес осадка стремится опустить его вниз. Поэтому, если имеется достаточная скорость для создания вихревых течений, чтобы удержать осадок во взвешенном состоянии, заиливание будет предотвращено.

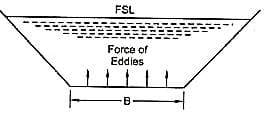
Сила вихревых течений согласно теории ила Кеннеди

Допущения относительно теории ила Кеннеди

Вихревое течение возникает из-за трения между текущей водой и шероховатостью дна канала.
Качество взвешенного ила пропорционально ширине дна.
Теория применима к тем каналам, которые протекают по дну, состоящему из песчаного ила или ила той же марки.

Критическая скорость на основе теории ила Кеннеди

Критическая скорость – это средняя скорость, при которой канал не заиливается и не размывается. Скорость зависит от глубины воды в канале. Общая форма критической скорости выглядит следующим образом:Где
Vo = критическая скорость
D = полная глубина водоснабжения, как показано на рис. 2.
C и n: константы, которые, как выяснилось, равны 0,546 и 0,64, соответственно.
Таким образом, уравнение 1 было переписано следующим образом:Более того, уравнение 2 еще более улучшилось после того, как стало ясно, что содержание ила влияет на критическую скорость. Поэтому был введен коэффициент, называемый коэффициентом критической скорости, и уравнение стало выглядеть следующим образом:Более того, уравнение 2 еще более улучшилось после того, как стало ясно, что содержание ила влияет на критическую скорость. Поэтому был введен коэффициент, называемый коэффициентом критической скорости, и уравнение стало выглядеть следующим образом:Где
m: коэффициент критической скорости, который равен отношению фактической скорости (V) к критической скорости (Vo), значение m приведено в таблице 1.
Таблица 1 Значения m в зависимости от типа ила
Облицовка канала
Значения N
Земля
0.0225
Каменная кладка
0.02
Бетон
0,013 – 0,018

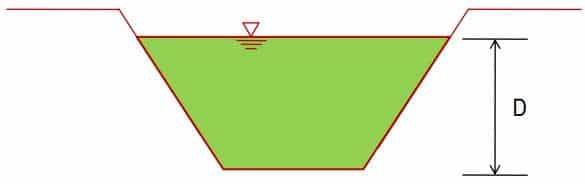
Глубина воды в канале

Ограничения иловой теории Кеннеди

Для проектирования канала с использованием теории ила Кеннеди использовался метод проб и ошибок.

Уравнения для оценки уклона дна не существует, поэтому для расчета уклона дна использовалось уравнение, разработанное Куттером.

Отношение ширины канала (B) к его глубине (D) не имеет значения в теории ила Кеннеди.

Не существует идеального определения для класса соли и солевого заряда.

Сложное явление транспортировки ила не полностью учтено, и только концепция критического отношения скоростей (m) считается достаточной.

Процедура проектирования канала с использованием иловой теории Кеннеди

Существует два случая проектирования канала с использованием иловой теории Кеннеди в зависимости от заданных данных. Оба случая представлены ниже:

Случай 1

Предварительно должны быть получены следующие данные:
расход (Q), коэффициент изрезанности (N), коэффициент критической скорости (m) и уклон дна канала (s).
1. Предполагается подходящая полная глубина питания (D).
2. Затем найдите среднюю скорость, используя уравнение Кеннеди (уравнение 3).
3. После этого найдите площадь поперечного сечения с помощью уравнения неразрывности:Где:
Q: расход
A: площадь поперечного сечения
V: средняя скорость, рассчитанная на этапе 2.
4. Предположим форму участка канала с боковыми уклонами (0. 5V:1H).
5. Определите значение ширины основания канала (B).
6. Затем найдите периметр канала (P). Это поможет определить среднюю гидравлическую глубину канала (R).Где:
R: средняя гидравлическая глубина
A: площадь поперечного сечения канала
P: периметр участка
7. Наконец, рассчитайте среднюю скорость (V), используя формулу Куттера: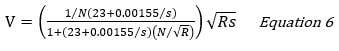Где:
N: коэффициент шероховатости в зависимости от типа материала облицовки канала. В таблице 2 приведены значения N для различных условий облицовки.
S: уклон дна, как 1 в ‘n’.
Оба значения V, рассчитанные по уравнению 3 и V, рассчитанные по уравнению 6, должны быть одинаковыми. В противном случае повторите описанную выше процедуру, приняв другое значение D.
Обычно пробная глубина принимается в пределах от 1 м до 2 м. Если условие не удовлетворяется в этих пределах, то оно может быть принято соответствующим образом.
Таблица 2 Значения N в зависимости от материала облицовки канала

Случай 2

Когда заданы расход (Q), коэффициент колейности (N), отношение критических скоростей (м) и отношение B/D.
1. Предположим, что B/D = X
2. Используя уравнение Кеннеди, найдите “V” в терминах D.
3. Найдите площадь поперечного сечения канала в терминах D2.
4. Используя уравнение непрерывности 4, найдите значение D., а затем найдите ширину основания (B).
5. Найдите среднюю гидравлическую глубину (R) с помощью уравнения 5.
6. Наконец, найдите значение “V” с помощью уравнения 3.
7. Подставив значение V из шага 6 в уравнение 6, вы получите продольный уклон канала (S). Этот случай будет выполняться методом проб и ошибок.

Читайте далее: