Тавровые балки образуются при монолитном бетонировании железобетонных плит перекрытий, крыш и настилов с несущими балками. Как правило, опалубка устанавливается для нижней и боковых сторон балок и софитов перекрытий. Загнутые стержни и ригели балки выдвигаются вверх в перекрытие. После этого все элементы заливаются одновременно, от самой нижней точки балки до верха перекрытия.
Часть перекрытия вокруг балки, называемая фланцем, будет работать вместе с балкой и противостоять продольной силе сжатия. Внутренние балки имеют фланцы с обеих сторон и называются Т-образными балками, а крайние балки имеют фланцы с одной стороны и называются Г-образными балками. Часть балки, выступающая под перекрытием, называется стержнем или полотном.
Конструкция железобетонных тавровых балок аналогична конструкции прямоугольных железобетонных балок, за исключением фланцев, которые необходимо учитывать в первом типе балок.
- Процедура проектирования
Эффективная ширина фланца
Для того чтобы начать процесс проектирования, необходимо определить эффективную ширину фланца (be) тавровой балки. На рисунке 1 фланец изолированной тавровой балки немного шире, чем стержень тавровой балки, и весь фланец эффективно сопротивляется сжатию.
Эффективная ширина фланца изолированной тавровой балки
Однако на рисунке 2 ширина фланца велика; следовательно, части фланцев, расположенные на расстоянии от стержня, не полностью участвуют в сопротивлении сжатию, и напряжения продолжают меняться.
Эффективная ширина фланца внутренней тавровой балки
Изменение напряжений приводит к утомительным расчетам, поэтому рассматривается равномерное распределение напряжений по меньшей ширине эффективного фланца, см. рисунок 3.
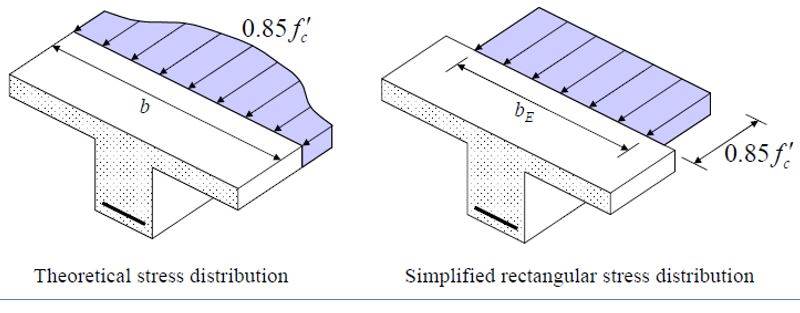Теоретическое распределение напряжений и упрощенное или прямоугольное распределение напряжений по ширине фланца тавровой балки
Согласно ACI 318-19, эффективная ширина фланца тавровой балки может быть определена следующим образом:
1. Изолированные балки
Для изолированных балок, в которых фланец используется только для обеспечения дополнительной площади сжатия, фланец должен иметь толщину больше или равную 1/2bw, а эффективную ширину меньше или равную 4bw.
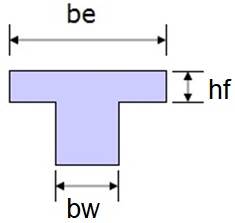Геометрия изолированной тавровой балки
2. Внутренние тавровые балки
Согласно стандарту 318-19, эффективная ширина фланца внутренней тавровой балки не должна превышать наименьшее из следующих значений:
1 – одной четвертой длины свободного пролета балки, L/4.
2- Ширина полотна плюс 16-кратная толщина перекрытия, bw +16hf .
3- Межцентровое расстояние между балками.
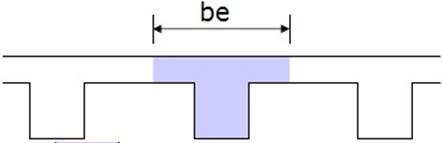Эффективная ширина фланца внутренней тавровой балки
3. Краевая балка (L-образная)
Согласно стандарту 318-19, эффективная ширина фланца краевой балки не должна превышать наименьшее из следующих значений:
1- Эффективная ширина фланца (должна быть) равна или меньше, чем (bw+(Clear span/4))
2- Эффективная ширина фланца (должна быть) равна или меньше, чем (bw+(6hf))
3- Эффективная ширина фланца (должна быть) равна или меньше, чем (bw+половина расстояния до следующего чистого полотна балки)
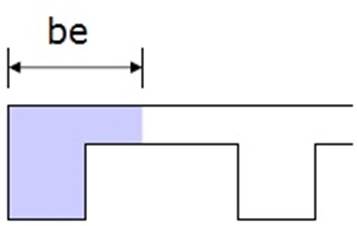Эффективная ширина фланца Г-образной балки
Т-образная балка в сравнении с прямоугольной балкой
Если к Т-образной железобетонной балке приложены отрицательные моменты на опорах, то балка проектируется как прямоугольное сечение, поскольку бетоном в напряжении пренебрегают. Ширина прямоугольного сечения равна ширине стержня (полотна), см. рисунок 7.
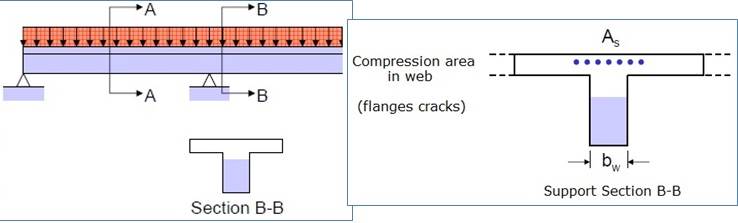Т-образная балка, подверженная отрицательному моменту
Однако, когда тавровая балка подвергается воздействию положительного момента, фланец находится в зоне сжатия, поэтому балка должна проектироваться как тавровая балка, см. рис. 8.
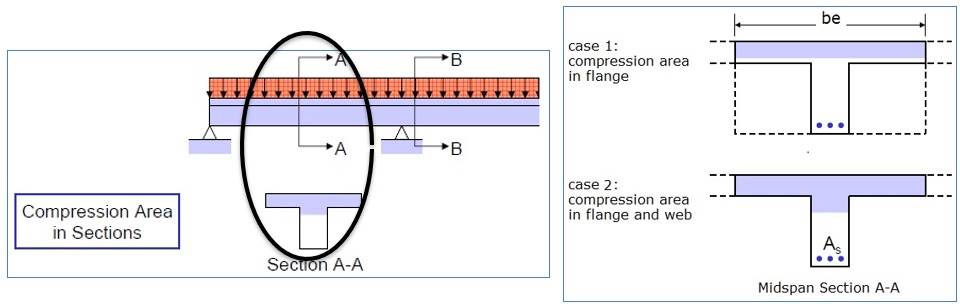Тавровая балка под действием положительного момента
Проектирование железобетонной тавровой балки
Проектирование балки таврового сечения включает расчет размеров (be, hf, h и bw) балки и необходимой площади армирования (As). Толщина фланца (hf) и ширина (be) обычно определяются при проектировании перекрытия.
На размер полотна или стержня балки влияют те же факторы, что и на размер прямоугольной балки. В случае непрерывной тавровой балки сжимающие напряжения бетона наиболее критичны в областях отрицательных моментов, где зона сжатия находится в стержне (полотне) балки.
Распределение напряжений в тавровой балке показано на рисунке 9:
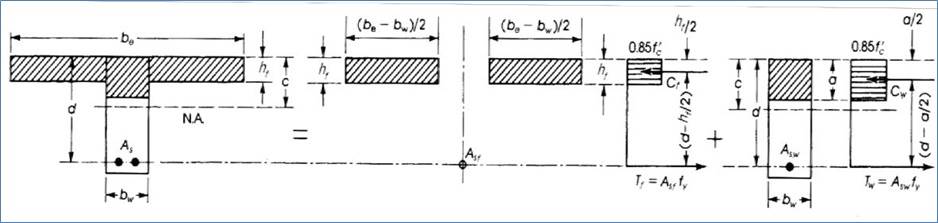Распределение напряжений в тавровой балке
Процедура проектирования
2. Определите эффективную ширину фланца (be)
3. Выберите размеры полотна (bw) и (h), основываясь либо на требованиях отрицательного изгиба на опорах, либо на требованиях сдвига.
4. Предположите, что a=hf , затем рассчитайте (As), используя следующее выражение:
5. Проверьте предполагаемое значение (a):
В уравнение 2 подставьте значение (be), найденное на этапе 2.
Если a< hf, спроектируйте балку как прямоугольное сечение и следуйте процедуре проектирования прямоугольной балки.
Если a> hf, спроектируйте балку таврового сечения и перейдите к шагу 6.
6. Вычислите площадь арматуры, необходимую для уравновешивания момента фланца по уравнению 3, а затем момента фланца по уравнению 4:
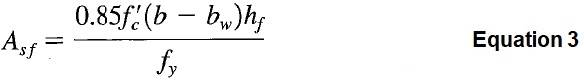
7. Вычислите момент полотна:
8. Предположите прямоугольную глубину блока напряжений (например, a= 100 мм), затем оцените площадь армирования (Asw), необходимую для уравновешивания момента полотна:
Значение (d) следует вычислить по следующей формуле:
d= высота балки- бетонное покрытие- диаметр стремена- 0,5*диаметр продольной стали Уравнение 7
Затем проверьте предполагаемую глубину прямоугольного блока напряжений (a), используя (Asw):
Используйте новое значение (a) и подставьте его в уравнение 6, затем вычислите новое значение (Asw). Повторяйте этот процесс до тех пор, пока не будет достигнуто правильное значение (Asw). Обычно достаточно трех опытов.
9. Вычислите общее значение As, которое равно (Asf+Asw), затем определите количество арматуры:
Количество стержней = As/площадь одного стержня Уравнение 9.
10. набросайте окончательный проект, на котором представлены все необходимые данные.
Где:
Пример:
Система перекрытия, показанная на рисунке 10, состоит из бетонной плиты толщиной 75 мм, опирающейся на бетонные тавровые балки с пролетом 7,5 м и центрами 1,2 м. Размеры полотна, которые определяются требованиями к отрицательным моментам на опорах, составляют bw= 275 мм и d= 500 мм. Какая площадь растяжения стали необходима в середине пролета для восприятия факторизованного момента 725 КН.м? Свойства материала: fc’= 21 МПа и fy= 420 МПа.
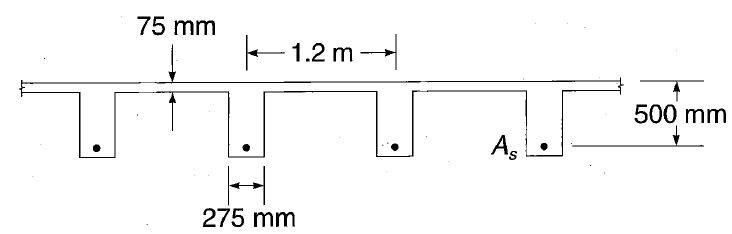Пример тавровой балки
Решение:
1. Приложенный момент обеспечен, Му= 725 КН.м
2. Найдите эффективную ширину фланца (be), которая является наименьшей из следующих:
- Span/4= 7500/4= 1875 мм
- bw+16hf= 275+16*75= 1475 мм
- Межосевое расстояние между балками = 1200 мм.
Следовательно, эффективная ширина фланца равна 1200 мм.
3. Размеры полотна приведены.
4. Предположим, a=hf= 75 мм, и примем коэффициент снижения прочности равным 0,9.
As= (725*106)/(0,9*420(500-0,5*75)= 4147,004 мм2.
5. Проверьте предполагаемое значение (a), используйте (As), вычисленное на этапе 4:
a=(4147,004*420)/(0,85*21*1200)= 81,31 мм.
Так как a= 81,31 мм> hf=75 мм, то балка должна быть спроектирована как тавровое сечение.
6. Вычислите (Asf) и фланцевый момент:
Asf= (0,85*21*(1200-275)*1200)/420= 2946,23 мм2
phi*Mnf= 2946.23*420*(500-0.5*75)*10-6= 572.23 KN.m
phi*Mnw=725-572.23= 209.54 KN.m
8. Рассчитайте площадь армирования (Asw), при условии, что a=100 мм и phi= 0,9
Asw= (209,54*106)/(0,9*420*(500-0,5*100)= 1231,86 мм2
проверьте (a), используя вышеприведенное значение (Asw),
a=(1231,86*420)/(0,85*21*275)= 105,4 мм
Найдите новое значение (Asw), используя a= 105,4 мм
Asw= (209,54*106)/(0,9*420*(500-0,5*105,4)= 1239,29 мм2
Поскольку новое значение Asw очень близко к предыдущему, дальнейшее испытание не требуется.
Asw=1239,29 мм2
9. Вычислите общее значение As, которое равно (Asf+Asw):
As= Asf+Asw= 2946,23+1239,29= 4180,29 мм2
Необходимо проверить принятый коэффициент снижения прочности:
Выбор одного стального стержня приводит к тому, что площадь армирования значительно превышает общую площадь. Следовательно, №. 32 и 29 стальных стержней выбираются для получения площади армирования, максимально приближенной к требуемой площади армирования.
Для этого три стержня диаметром 32 мм, и соответствующая площадь армирования составляет 2457 мм2
Имеются три три стержня диаметром 29 мм, и соответствующая площадь армирования составляет 1935 мм2
Общая площадь армирования равна 4349 мм2; это и есть ответ на вопрос.
Итак, стальные стержни расположены в два слоя, а расстояние между двумя слоями равно 25 мм.
Проверьте коэффициент снижения прочности:
Так как прочность бетона на сжатие меньше 30 МПа, следовательно, B1=0,85
глубина нейтральной оси (c)= a/B1= 105,4/0,85= 124 мм
dt: расстояние от грани сжатия балки до центра нижнего слоя стальных стержней:
c/dt= 124/525= 0,236<0,375. Следовательно, предположение верно.
Для получения более подробной информации о расчете коэффициента снижения прочности, пожалуйста, нажмите здесь
Часто задаваемые вопросы
Что такое железобетонная тавровая балка?
Как правило, железобетонная система перекрытий состоит из балок и плиты, которые строятся монолитно. В результате часть перекрытия вокруг верхней части балки работает вместе, чтобы нести нагрузку. По сути, балки имеют дополнительную ширину в верхней части, которая называется фланцами. Такая балка называется тавровой.
Какова эффективная ширина фланца в железобетонной тавровой балке?
Эффективная ширина фланца состоит из ширины полотна балки плюс ширина фланца с каждой стороны балки. Распределение напряжений по ширине эффективной ширины фланца является равномерным.
Что такое эффективная глубина железобетонной балки?
Эффективная глубина равна расстоянию от крайнего волокна сжатия балки до центра тяжести стальных стержней, заделанных в балку.
Проектирование прямоугольной железобетонной балки
Основы проектирования балок
Читайте далее:- Как спроектировать одностороннее перекрытие в соответствии с ACI 318-19? | Прилагается пример.
- Стальные гофрированные полотна в мостовых балках.
- Проектирование прямоугольной железобетонной балки.
- Типы систем перекрытий для строительства многоэтажных стальных конструкций.
- Минимальное и максимальное соотношение армирования в различных железобетонных элементах.
- 21 Виды балок в строительстве [PDF].
- Мосты с пластинчатыми балками – детали и требования к конструкции.