Расчет чистой площади и допустимых напряжений для растягивающих элементов

РАСЧЕТ ПЛОЩАДИ НЕТТО ДЛЯ НАПРЯЖЕННЫХ ЭЛЕМЕНТОВ

Когда напряженные элементы сращиваются или соединяются с пластиной заклепками или болтами, часть материала удаляется из поперечного сечения из-за отверстий под болты или заклепки. Площадь нетто в любом сечении равна площади брутто минус вычет на отверстия в этом сечении. Вычет на отверстия равен произведению диаметра отверстия и толщины материала.

Чистая эффективная ширина,

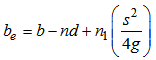
Где, s = шаг, т.е. расстояние между двумя последовательными заклепками в зигзагообразной цепи, измеренное параллельно направлению напряжения в элементе,

g = мерное расстояние

n = количество отверстий под заклепки

= количество зигзагов или наклонных линий.

Этот метод может быть применен также к уголкам, в которых ряды заклепок в обеих ножках расположены в шахматном порядке по отношению друг к другу. Для уголков ширина брутто должна быть равна сумме ширины ножек за вычетом толщины. Размер отверстий в противоположных ножках должен быть равен сумме размеров задней части уголков за вычетом толщины.

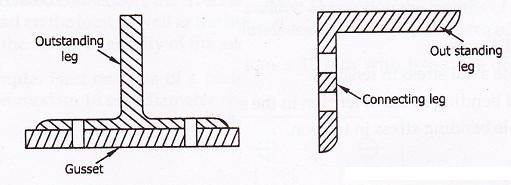
Чистое эффективное сечение для углов и тройников при растяжении

Угол обычно соединяется с опорной плитой одной ножкой, а тройник соединяется только через фланец.

Натяжные элементы

ПРИМЕР – 1

В случае одиночного растянутого уголка, соединенного только одной ножкой,

Чистая эффективная площадь =

где площадь соединенной ноги,

= площадь выдающейся ноги, и

Для угловых сечений – a x b x t,

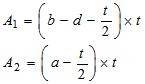
При использовании уголков с ушками можно рассматривать чистую площадь сечения всего углового элемента.

ПРИМЕР – 2

В случае пары уголков, расположенных спина к спине (или одного тройника) при растяжении, соединенных только одной ножкой на каждом уголке (или фланцем тройника) с одной и той же стороной пластины,

Чистая эффективная площадь =

где площадь соединенных ног (или фланца тройника)

= площадь выдающейся ножки (или полотна тройника), и

ПРИМЕР – 3

В случае двойных углов или тройников с прямым натяжением, расположенных спина к спине и соединенных с обеих сторон ластовицей,

Чистая эффективная площадь = общая площадь сечения – площадь отверстий

ДОПУСТИМЫЕ НАПРЯЖЕНИЯ ПРИ ОСЕВОМ РАСТЯЖЕНИИ

Оно связано с гарантированным минимальным пределом текучести стали с соответствующим коэффициентом безопасности. В большинстве сводов правил коэффициент безопасности принимается равным 1,67.

Прямое напряжение при осевом растяжении или эффективная площадь сетки не должна превышать определяемое уравнением,

Где, = минимальный предел текучести стали в = минимальный предел текучести стали в (МПа).

Индийский стандарт IS: 226

Он устанавливает следующие допустимые напряжения при осевом растяжении для стали,

(i)

Пластины, уголки, тройники, двутавровые балки, швеллеры и плоские профили

толщиной до 20 мм включительно

150 МПа

толщиной свыше 20 мм до 40 мм

144 МПа

Толщина свыше 40 мм

138 МПа

(ii)

Прутки (круглые, квадратные и шестигранные)

Диаметр до 20 мм включительно

150 МПа

Свыше 20 мм в диаметре

144 МПа

Допустимое комбинированное напряжение

Когда напряженные элементы подвергаются как осевой нагрузке, так и изгибающему моменту, то допустимое напряжение определяется по формуле,

где, = осевое растягивающее напряжение,

= допустимое осевое напряжение при растяжении,

= расчетное напряжение изгиба при растяжении в крайнем волокне, и

= допустимое напряжение изгиба при растяжении.

• ПРОЕКТИРОВАНИЕ СТАЛЬНЫХ КОМПРЕССИОННЫХ ЭЛЕМЕНТОВ.
• Типы сборных элементов и систем для строительства мостов.
• Типы напрягаемых элементов в конструкциях из конструкционной стали.
• Подготовительные мероприятия для выполнения клепки и болтов.
• Процедура проектирования железобетонной тавровой балки с примером.
• Теория линии текучести для проектирования перекрытий – допущения, методы анализа.
• Как выполнить клепку и болты в стальной конструкции?.