Брусья различного сечения, свойств материала и размеров, которые подвергаются осевым нагрузкам, могут быть проанализированы для определения соответствующих значений напряжений и деформаций.
Анализ выполняется на основе фундаментального уравнения из закона Гука, которое связывает напряжение (f) и деформацию (e) следующим образом
f = e.E ———-Eq.1
Где “E” – модуль упругости. Здесь кратко объясняется анализ деформации или деформации стержней различного сечения.
Читайте также: Различные упругие константы и их взаимосвязь
Анализ стержней разного сечения
Рассмотрим пруток различной длины, площади сечения и диаметра, подверженный осевой нагрузке ‘P’, как показано на рисунке 1.
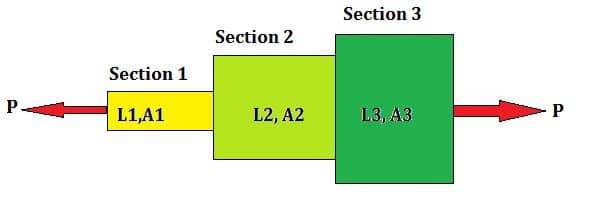 Рис.1. Пруток переменного сечения
Рис.1. Пруток переменного сечения
Напряжение и деформация длины, возникающие в каждом из сечений прутка, различны, даже если осевая нагрузка, действующая на пруток, одинакова. При выводе следует принцип,
Общее изменение длины, dL = сумма изменений длины секции 1, секции 2 и секции 3.
dL = dL1 + dL2 +dL3 ———-Eq.2
1. Анализ секции 1
Напряжение в секции 1,
f1 = Нагрузка/площадь секции-1 = P/A1
Деформация в секции 1,
e1 = Изменение длины/Оригинальная длина = dL1/L1 = f1/E = P/(A1E) [Из уравнения 1].
Следовательно, изменение длины dL1=PL1/(A1E) ———-Eq.3
2. Анализ секции 2
Напряжение в секции 2,
f2 = Нагрузка/площадь секции-2 = P/A2
e2 = Изменение длины/Оригинальная длина = dL2/L2 = f2/E =P/(A2E) [Из уравнения 1].
Следовательно, изменение длины dL2= PL2/(A2E) ———-Eq.4
Напряжение в секции 3,
f3 = Нагрузка/площадь секции 3 = P/A3
e3 = Изменение длины/Оригинальная длина = dL3/L3 = f3/E=P/(A3E) [Из уравнения 1].
Следовательно, изменение длины dL3= PL3/(A3E) ———-Eq.5
Из уравнения 2,
dL = dL1 + dL2 +dL3
Следовательно, уравнение 3 + уравнение 4 + уравнение 5,
dL = dL1 + dL2 +dL3 = PL1/(A1E) +PL2/(A2E)+ PL3/(A3E)
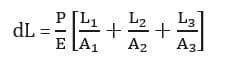 Уравнение 6
Уравнение 6
Приведенное выше уравнение используется, когда участки бруса имеют одинаковый модуль упругости. Если значение ‘E’ разное, мы получаем соотношение,
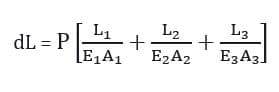 Экв.2
Экв.2
Читайте также: Зависимость между напряжением и деформацией бетона
Читайте также: Зависимости между напряжениями и деформациями стальных стержней
Читайте далее:- Различные упругие константы и их взаимосвязь.
- Что такое арматура? Типы и марки стальной арматуры.
- Испытание на растяжение стального стержня – процедура и результаты.
- Анализ фермы с примерами.
- ПРОЕКТИРОВАНИЕ СТАЛЬНЫХ КОМПРЕССИОННЫХ ЭЛЕМЕНТОВ.
- 14 видов прокатных стальных профилей – формы, размеры и свойства.
- График гибки стержней подножия (BBS) – оценка количества стали.