Анализ фермы с примерами

Изучите методы анализа ферм с примерами. В статье рассказывается об анализе ферм методами соединений и методами сечений.
Мы знаем основы равновесия тел; теперь мы обсудим фермы, которые используются для создания устойчивых несущих конструкций. В качестве примера можно привести боковые стороны мостов или высокие телебашни или вышки, по которым проходят провода электропередач. Схема конструкции на боковой стороне моста изображена на рисунке 1.

Структура, показанная на рисунке 1, по сути, является двумерной структурой. Она известна как плоская ферма. С другой стороны, вышка микроволновой печи или мобильного телефона представляет собой трехмерную конструкцию. Таким образом, существует две категории ферм – плоские фермы, как на сторонах моста, и пространственные фермы, как на телебашнях. В этом курсе мы сосредоточимся на плоских фермах, в которых базисные элементы прикреплены друг к другу в плоскости.
Чтобы мотивировать структуру плоской фермы, возьмем тонкий стержень (12) между точками 1 и 2 и прикрепим его к неподвижному штыревому соединению в точке 1 (см. рисунок 2).

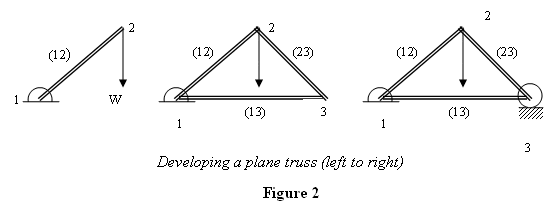
Теперь я поставлю штифт (pin2) в точке 2 на верхнем конце и подвешу к нему груз W. Вопрос в том, если мы хотим удержать груз в этой точке, какие еще минимальные опоры мы должны обеспечить? Для стержней мы должны сделать только штыревые соединения (Мы предполагаем, что все находится в этой плоскости и конструкция не опрокидывается набок). Поскольку стержень (12) имеет тенденцию вращаться по часовой стрелке, мы остановим движение точки 2 вправо, соединив ее со стержнем (23), а затем остановим движение точки 3 вправо, соединив ее с точкой 1 другим стержнем (13). Все шарниры в этой конструкции – штифтовые. Однако, несмотря на все это, вся конструкция все еще имеет тенденцию поворачиваться по часовой стрелке, потому что на нее действует крутящий момент из-за W. Чтобы противостоять этому, мы прикрепляем колесо к точке 3 и ставим его на землю. Это тот минимум, который необходим для удержания груза на месте. Треугольник, образованный стержнями, составляет основу плоской фермы.
Примечание: Здесь может возникнуть вопрос, зачем нам нужен горизонтальный стержень (13). Потому что иначе точка 3 будет постоянно смещаться вправо, делая всю конструкцию неустойчивой. На стержень (13) действуют две силы: одна вертикальная сила, обусловленная колесом, и другая на конце 2. Однако эти две силы не могут быть коллинеарными, поэтому без стержня (13) система не будет находиться в равновесии. Как правило, в ферме каждый шарнир должен быть связан как минимум с тремя стержнями или двумя стержнями и одной внешней опорой.
Давайте теперь проанализируем силы в только что созданной структуре. Для простоты я принимаю длины всех стержней равными. Чтобы получить силы, я рассматриваю все силы на каждом стержне и нахожу условия, при которых стержни находятся в равновесии. Прежде всего отметим, что каждый стержень находится в равновесии под действием двух сил, приложенных штифтами на их концах. Как я уже говорил в предыдущей лекции, в данной ситуации силы должны быть коллинеарны и, следовательно, направлены только вдоль стержней. Таким образом, каждый стержень находится под действием растягивающей или сжимающей силы. Таким образом, стержни (12), (23) и (13) испытывают силы, как показано на рисунке 3.

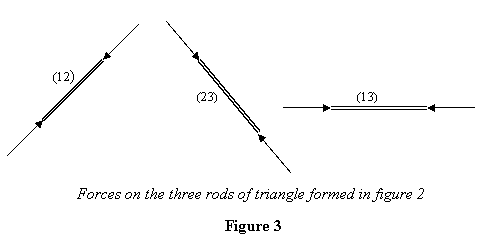
Обратите внимание, что мы приняли все силы за сжимающие. Если на самом деле силы растягивающие, то ответ будет отрицательным. Теперь рассмотрим штифт 2. На штифт 2 действуют только силы F12, вызванные стержнем (12), и F23, вызванные стержнем (23). Кроме того, его тянет вниз масса W. Таким образом, силы, действующие на штифт 2, выглядят так, как показано на рисунке 4.

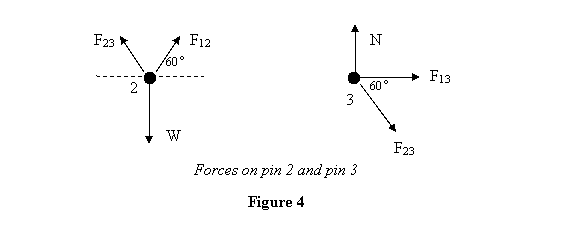
Применение условия равновесия к штифту (2) дает

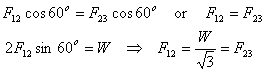
Теперь рассмотрим штифт 3 (см. рисунок 4). Он находится в равновесии под действием сил F23, нормальной реакции N и горизонтальной силы F13.
Применение условия равновесия дает

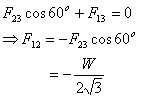
Поскольку направление F13 получается отрицательным, направление должно быть противоположным предполагаемому. Баланс сил в вертикальном направлении дает

Таким образом, мы видим, что вес удерживается этими тремя стержнями. Структура является детерминированной и удерживает груз на месте.
Даже если мы заменим штифтовые соединения маленькой пластиной (известной как ласточкина пластина) с двумя или тремя штифтами в них, анализ остается практически таким же, потому что штифты расположены так близко друг к другу, что они почти не создают момента в соединениях. Даже если стержни сварены вместе на стыках, с большой степенью точности большая часть силы передается в продольном направлении на стержни, хотя некоторый очень маленький (пренебрежимо малый) момент создается на стыках и может быть при возможном изгибе стержней.
Теперь мы готовы построить ферму и проанализировать ее. Мы будем строить ее, складывая все больше и больше треугольников вместе. Как видите, когда мы складываем эти треугольники, количество шарниров j и количество элементов (стержней) m связаны следующим образом:

m = 2j – 3

Это делает ферму статически определимой. Это легко понять следующим образом. Сначала рассмотрим всю ферму как единую систему. Если она должна быть статически определимой, то на нее должны действовать только три неизвестные силы, поскольку для сил в плоскости существуют три условия равновесия. Закрепление одного из ее концов штифтовым соединением и надевание другого на ролик делает это (ролик также дает дополнительное преимущество, поскольку он может помочь в регулировке любого изменения длины элемента вследствие деформаций). Если мы хотим определить эти внешние силы и силу в каждом члене фермы, общее количество неизвестных становится m + 3. Мы решаем эти неизвестные, записывая условия равновесия для каждого стержня; таких уравнений будет 2j. Чтобы система была детерминированной, мы должны иметь m + 3 = 2j , что и является условием, приведенным выше. Если мы добавим еще какие-либо члены, то они окажутся лишними. С другой стороны, меньшее количество элементов сделает ферму неустойчивой, и она разрушится при нагрузке. Это произойдет потому, что ферма не сможет обеспечить необходимое количество сил для выполнения всех условий равновесия. Статически детерминированные фермы известны как простые фермы.
Упражнение 1: На рисунке 5 показаны три часто используемые фермы на боковых сторонах мостов. Покажите, что все три фермы являются простыми фермами.

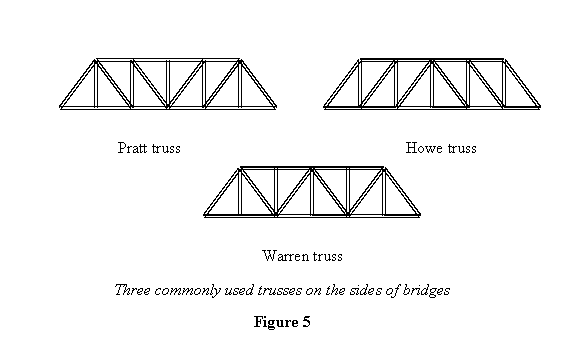
Вы можете спросить, зачем мы устанавливаем фермы на мостах. Как покажет наш последующий анализ, они распределяют нагрузку на все элементы и тем самым делают мост прочнее.
Теперь мы хотим получить силы, возникающие в различных элементах фермы при внешней нагрузке. Это можно сделать при следующих предположениях:

Существует два метода определения усилий в элементах фермы – метод соединений и метод сечений. Мы начнем с метода соединений:

Анализ фермы – метод шарниров:

В методе шарниров мы рассматриваем равновесие штыря в шарнирах. Поскольку силы на штыре одновременны, уравнения моментов не существует, а есть только два уравнения равновесия, а именно. . Поэтому мы начинаем наш анализ с точки, где имеется одна известная нагрузка и максимум две неизвестные силы. Вес каждого элемента делится на две половины и поддерживается каждым штифтом. В какой-то степени мы уже упоминали этот метод при изучении ферм. Давайте проиллюстрируем его на двух примерах.
Пример 1: В качестве первого примера возьмем ферму ABCDEF, как показано на рисунке 6, и нагрузим ее в точке E силой 5000 Н. Длина малых элементов фермы равна 4 м, а длина диагональных элементов равна m. Теперь я найду силы в каждом элементе этой фермы, предполагая, что они невесомы.

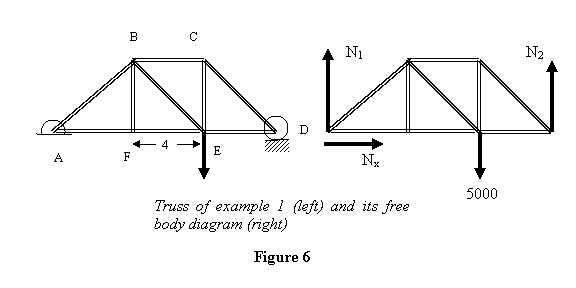
Возьмем каждую точку за штифтовое соединение и начнем уравновешивать силы на каждом из штифтов. Поскольку на штифт E действует внешняя нагрузка 5000 Н, можно начать с него. Однако в точке E имеется более двух неизвестных сил, поэтому мы не можем начать с точки E. Поэтому мы сначала рассмотрим ферму как единое целое и найдем реакции грунта в точках A и D, потому что тогда в точках A и D останется только две неизвестные силы. Горизонтальная реакция Nx в точке A равна нулю, так как на систему не действует внешняя горизонтальная сила. Чтобы найти N2, возьмем момент относительно точки A и получим

что через уравнение дает

В методе шарниров давайте теперь начнем с точки A и уравновесим различные силы. Мы уже предполагаем направление и показываем их приблизительно в точке A (рис. 7). Все углы, которые образуют диагонали, равны 45°.

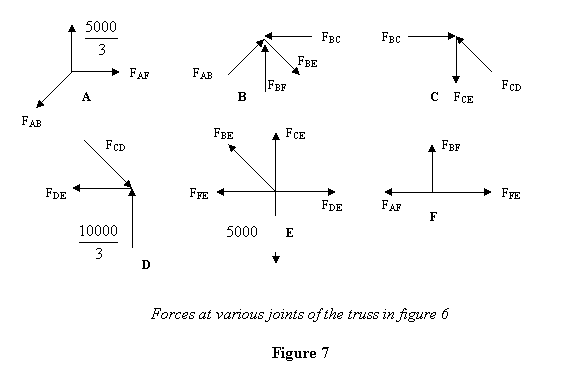
Единственные уравнения, которые нас теперь волнуют, это уравнения баланса сил.

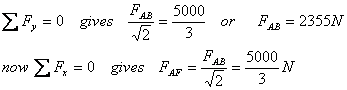
Помните, что силы на элементах AB и AF будут противоположны силам на штифте (III закон Ньютона). Поэтому сила на члене AB является сжимающей (отталкивает штифт A), а на AF – растягивающей (притягивает A к себе).
Далее я рассматриваю соединение F, где сила AF известна, а две силы BF и FE неизвестны. Для точки F

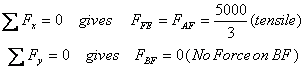
Далее я перехожу к точке B, так как теперь там есть только две неизвестные силы. В точке B

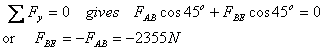
Отрицательный знак показывает, что в то время как мы показали, что сила FBE является сжимающей, на самом деле она является растягивающей.

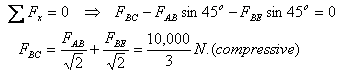
Далее я рассматриваю точку C и уравновешиваю силы в ней. Я уже предвидел направление сил и показал, что FCE будет растягивающей, а FCD – сжимающей.

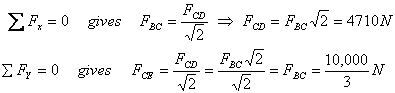
Далее я перехожу к точке D, где нормальная реакция составляет N и уравновешиваю силы там.

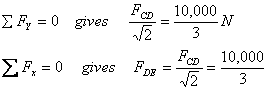
Таким образом, были определены силы в различных элементах фермы. К ним относятся

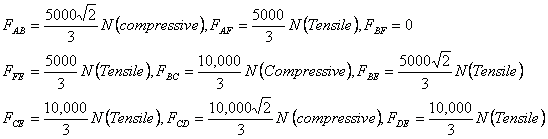
Вам может быть интересно, как мы получили все силы без использования уравнений на всех шарнирах. Вспомните, что именно так мы получили условие статической детерминации. Нам не нужно было использовать все суставы, потому что мы уже рассматривали систему как единое целое и получили два уравнения. Поэтому один шарнир – в данном случае E – не нужно анализировать. Однако, учитывая, что ферма статически определима, все эти силы должны уравновешиваться в точке E, где была приложена нагрузка. Я оставлю это в качестве упражнения для вас. Далее я спрошу, как изменится ситуация, если каждый член фермы будет иметь вес. Предположим, что каждый элемент весит 500 Н, тогда при условии, что нагрузка делится поровну между двумя штырями, удерживающими элемент, нагрузка на ферму будет выглядеть так, как показано на рисунке 8 (нагрузка от веса показана красным цветом). За исключением точек A и D нагрузка от веса равна 750 Н; в точках A и D она равна 500 Н.

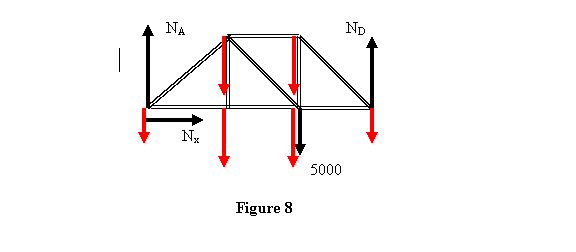
Теперь внешняя реакция на каждом конце будет равна.

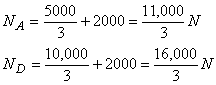
Дополнительные 2000 Н можно вычислить либо из уравнения моментов, либо сразу, поняв, что новый дополнительный вес абсолютно симметричен относительно центра фермы и поэтому будет поровну распределен между двумя опорами. Для уравновешивания сил на других опорах, мы следуем той же процедуре, что и выше, помня, однако, что на каждую опору теперь действует внешняя нагрузка из-за веса каждого элемента. Я буду решать для сил в некоторых элементах фермы. Рассматривая точку A, мы получаем

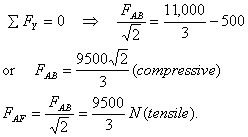
Далее переходим к точке F и видим, что силы равны

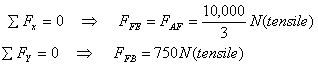
Аналогично можно решить для других штырей фермы, и я оставляю это упражнение для вас.
Продемонстрировав вам метод шарниров, перейдем к рассмотрению метода сечений, который непосредственно дает силу, действующую на нужный элемент фермы.

Анализ фермы – метод сечений:

Как следует из названия, в методе сечений мы делаем разрезы через ферму и затем вычисляем усилия в элементах фермы, через которые сделан разрез. Например, если я возьму задачу, которую мы только что решили методом соединений, и сделаю разрез S1, S2 (см. рис. 9), мы сможем определить силы в членах BC, BE и FE, рассматривая равновесие части слева или справа от разреза.

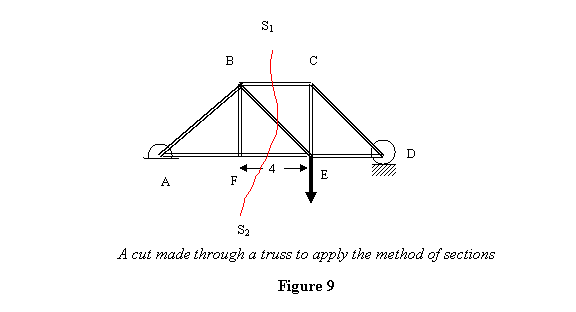
Позвольте мне проиллюстрировать это. Как и в методе шарниров, мы начинаем с определения реакций на внешней опоре фермы, рассматривая ее как целое жесткое тело. В данном конкретном случае это дает N в точке D и N в точке A. Теперь рассмотрим участок фермы слева (см. рис. 10).

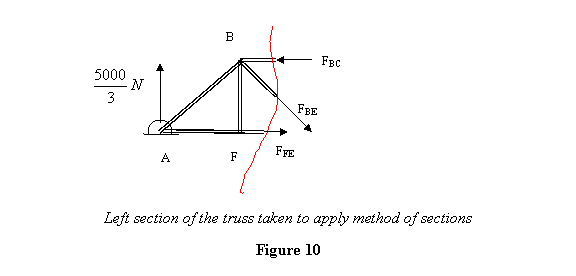
Поскольку вся эта секция находится в равновесии, . Обратите внимание, что теперь мы используем все три уравнения для равновесия, так как силы в отдельных элементах не совпадают. О направлении силы в каждом члене можно догадаться путем осмотра. Таким образом, сила в сечении членов BE должна быть направлена вниз, потому что нет другого члена, который мог бы дать направленную вниз силу, чтобы уравновесить N реакции в точке А. Это ясно говорит нам, что F BE растягивается. Аналогично, чтобы противодействовать крутящему моменту вокруг B, создаваемому N в точке A, сила на FE также должна быть направлена от F к E. Таким образом, эта сила также является растягивающей. Если мы рассмотрим баланс крутящего момента вокруг A, N и FFE не дают никакого момента относительно А. Поэтому для противодействия моменту, создаваемому FBE, сила на BC должна действовать в направлении В, делая силу сжимающей.
Давайте теперь рассчитаем отдельные силы. Легче всего вычислить FFE. Для этого возьмем момент относительно В. Это дает
4 × = 4 × F FE
F FE = N
Далее вычисляем FBE . Для этого используем уравнение . Оно дает

Наконец, чтобы рассчитать FBC, мы можем использовать либо уравнение относительно A или

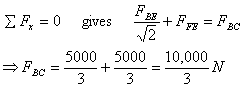
Таким образом, мы определили силы в этих трех элементах непосредственно, без расчета сил, идущих от одного соединения к другому соединению, и сэкономили много времени и усилий в процессе. Силы, действующие на правое сечение, будут противоположны силам, действующим на левые сечения в точках, через которые проходит сечение. Это можно использовать для проверки нашего ответа, и я оставляю это как упражнение для вас.
После этой иллюстрации позвольте мне изложить шаги, которые предпринимаются для решения сил в элементах фермы методом сечений:
1. Сделайте разрез, чтобы разделить ферму на секции, пропуская разрез через элементы, где требуется сила.
2. Сделать разрез по трем элементам фермы, так как при наличии трех уравнений равновесия, т.е. трех уравнений равновесия. мы можем решить максимум для трех сил.
3. Применить условия равновесия и решить для нужных сил.
При применении метода сечений изобретательность заключается в том, чтобы сделать правильный разрез. Этот метод позволяет непосредственно вычислить требуемую силу, избегая тяжелой работы, связанной с применением метода шарниров, когда необходимо решать для каждого шарнира.

• Проектирование кровельных ферм.
• Детерминированные и неопределенные структуры и их различия.
• Анализ рамы с сопротивлением моменту и распределение боковой нагрузки.
• Основные концепции устойчивости конструкции.
• Типы мостов по пролетам, материалам, конструкциям, функциям, полезности и т.д..
• Метод распределения моментов в структурном анализе.
• Катастрофа моста Пойнт Плезант: Обрушение подвесного моста с цепью для глаз.