Метод распределения моментов в структурном анализе

Метод распределения моментов предлагает удобный способ анализа статически неопределимых балок и жестких рам. В методе распределения моментов каждый шарнир анализируемой конструкции фиксируется таким образом, чтобы создать фиксированные конечные моменты.
Затем каждый фиксированный шарнир последовательно освобождается, и фиксированные конечные моменты (которые к моменту освобождения не находятся в равновесии) распределяются на соседние элементы до достижения равновесия.
Более того, метод распределения моментов в математических терминах можно представить как процесс решения набора одновременных уравнений с помощью итерации. Кроме того, он относится к категории методов структурного анализа, основанных на перемещении.
Наконец, метод распределения моментов в структурном анализе подробно представлен в следующих разделах, а также приведен пример решения.

Основные определения терминов в методе распределения моментов в структурном анализе

Моменты в неподвижных концах

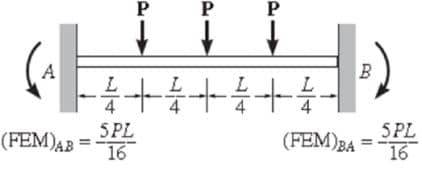
Моменты от неподвижных концов – это моменты, возникающие на концах элементов при закреплении соединений. В таблице 1 приведены уравнения для вычисления моментов в неподвижных концах.
Таблица 1: Уравнения для расчета неподвижных моментов

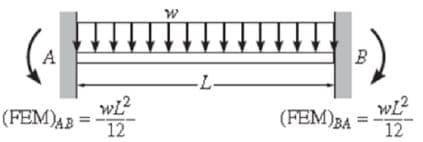
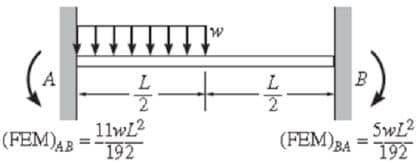
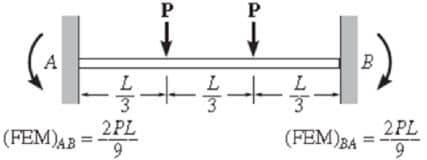
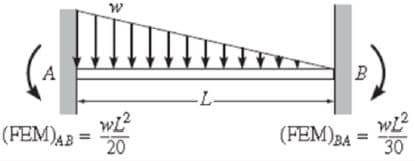
Жесткость при изгибе

Жесткость при изгибе (EI/L) элемента представлена как произведение модуля упругости (E) и второго момента площади (I), деленное на длину (L) элемента. Кроме того, в методе распределения моментов требуется не точное значение, а отношение жесткостей изгиба всех элементов.

Коэффициенты распределения

Коэффициенты распределения могут быть определены как пропорции несбалансированных моментов, переносимых каждым из членов.

Коэффициенты переноса

Несимметричные моменты переносятся на другой конец элемента при разжатии шарнира. Отношение перенесенного момента на другом конце к фиксированному моменту начального конца является коэффициентом переноса.
Наконец, для призматических элементов переносимый момент в каждом пролете имеет тот же знак, что и момент конца распределения, но в два раза меньше.

Условное обозначение

Любой момент, действующий по часовой стрелке, считается положительным. Это отличается от обычного инженерного знака, в котором используется декартова система координат с положительной осью x вправо и положительной осью y вверх, в результате чего положительный момент относительно оси z направлен против часовой стрелки.

Распределение момента и сравнение общепринятой системы координат

Каркасные конструкции

Рамные конструкции с боковыми стенками или без них могут быть проанализированы с помощью метода распределения моментов.

Процедура анализа распределения моментов для балки

1. Сдерживание всех возможных перемещений.
2. Затем вычислите коэффициенты распределения:
Коэффициент распределения DFi элемента, соединенного с любым шарниром J, равен

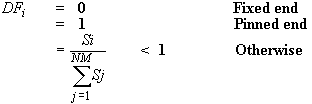
где S – вращательная жесткость, и оценивается по:

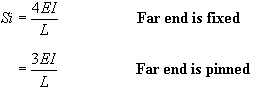
3. После этого определите коэффициенты переноса

Коэффициент переноса к неподвижному концу всегда равен 0,5, в противном случае он равен нулю.
4. Далее вычислите моменты неподвижного конца. (Таблица 1).
Они могут быть вызваны нагрузками в пролете, изменением температуры и/или относительным смещением между концами элемента.
5. Затем проведите циклы распределения для всех соединений одновременно.
6. Каждый цикл состоит из двух этапов:
Распределение выходящих из равновесия моментов Мо, где

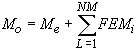
Тогда;

где

Me: внешний момент, приложенный к суставу (если есть)

Mo: общий момент вне равновесия на шарнире

FEMi: момент, приложенный к неподвижному концу

Mi: момент, распределенный на любой член

DFi: коэффициент распределения члена i

7. Вычисление переносимого момента на дальнем конце каждого элемента.
Процедура прекращается, когда на всех шарнирах момент выхода из равновесия имеет пренебрежимо малое значение. В этом случае шарниры должны быть сбалансированы и моменты переноса не вычисляются.
8. Наконец, вычислите окончательный момент на каждом конце каждого элемента.
Это сумма всех моментов (включая FEM), вычисленных во время циклов распределения.

Анализ статически неопределимой балки методом распределения моментов

• Элементы AB, BC, CD имеют одинаковую длину. .
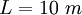• Изгибные жесткости равны EI, 2EI, EI соответственно.
• Концентрированная нагрузка величиной 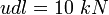действует на расстоянии 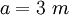от опоры A.
• Равномерная нагрузка интенсивности 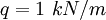действует на BC.
• Член CD нагружен в середине пролета сосредоточенной нагрузкой величиной .

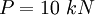Пример неопределимой балки

Моменты на концах балки

В следующих расчетах моменты против часовой стрелки положительны:










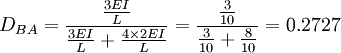
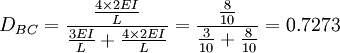
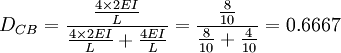
Коэффициенты распределения для шарниров A и D равны DAB = DDC = 1.
Коэффициенты переноса составляют , за исключением коэффициента переноса от D (неподвижная опора) к C, который равен нулю.

Детали расчетов

Таблица 2: детали расчетов распределения моментов
Соединения

A

B

C

D

Коэффициенты распределения
0
1
0.2727
0.7273
0.6667
0.3333
Моменты фиксированных концов
14.700
-6.300
8.333
-8.333
12.500
-12.500
Шаг 1
-14.700
-7.350
Шаг 2
1.450
3.867
1.934
Шаг 3
-2.034
-4.067
-1.017
Шаг 4
0.555
1.479
0.739
Шаг 5
-0.246
-0.493
-0.123
Шаг 6
0.067
0.179
0.090
Шаг 7
-0.030
-0.060
-0.015
Шаг 8
0.008
0.022
0.011
Шаг 9
-0.004
-0.007
-0.002
Шаг 10
0.001
0.003
Сумма моментов
-11.569
11.569
-10.186
10.186
-13.657

Результаты

Моменты в стыках, определенные методом распределения моментов




Здесь используется условный знак инженера, т.е. положительные моменты вызывают удлинение в нижней части балки.

Диаграмма сдвигающей силы и изгибающего момента

В таблице 3 приведена диаграмма сдвига и момента для анализируемой балки. Обратите внимание, что метод распределения моментов определяет только моменты на стыках.
Более того, построение полной диаграммы изгибающих моментов требует дополнительных расчетов с использованием определенных моментов в стыках и равновесия внутреннего сечения.
Таблица 3: диаграмма сдвигающих усилий и моментов для анализируемой неопределимой балки
Диаграмма сдвигающей силы

Диаграмма изгибающего момента

Результат метода распределения моментов в сравнении с результатом метода матрицы жесткости

Для сравнения ниже приведены результаты для того же пучка с использованием матричного метода. Как можно заметить из приведенного выше анализа, итерационный процесс проводился с точностью >0,01. Удивительно, но тот факт, что результаты матричного анализа и результаты анализа распределения моментов совпадают с точностью до 0,001, является простым совпадением.
Моменты в соединениях, определенные матричным методом

• Часовая башня Биг-Бен: тиканье с наклоном.
• Анализ фермы с примерами.
• Детерминированные и неопределенные структуры и их различия.
• Анализ рамы с сопротивлением моменту и распределение боковой нагрузки.
• Качественный структурный анализ балок и рам.
• Основные концепции устойчивости конструкции.
• Что такое неопределимые арки в строительстве?.