Качественный структурный анализ может быть не знаком инженерам-конструкторам. Обычным способом анализа конструкций является численный (количественный) метод, при котором конструкторы должны определить значения размеров и нагрузок и вычислить изгибающие моменты и реакции.
Однако перед численным анализом конструкций существует важный этап, который называется предварительным анализом. На этом этапе размеры элементов должны быть приняты до проведения анализа.
Естественно, подробный численный анализ проводится для проверки значений, которые были использованы в предварительном анализе. Поэтому, если размеры элементов конструкции не определены правильно, анализ придется повторять много раз, независимо от того, используется компьютер или ручной расчет. Это может отнять много времени и средств, и проектировщик должен постараться избежать такой ситуации.
По большому счету, считается, что необходимые знания и навыки для проведения подходящего и правильного предварительного анализа появляются в результате исследования и изучения методов численного анализа, но это может быть не так.
Качественный структурный анализ дает необходимые навыки и знания для проведения предварительного анализа. Основой этих навыков является понимание или распознавание отношений между нагрузками и результирующим поведением конструкции.
Например, в простых элементах основные навыки заключаются в распознавании взаимосвязей между нагрузками, отклоненной формой и результирующими реакциями.
Качественный структурный анализ существенно отличается от количественного метода. Он не только не имеет конкретной процедуры решения, но и зависит от ряда диаграмм.
В качественном анализе процедура зависит от задачи, например, в конкретной задаче может быть уместно начать решение с формы прогиба, в то время как для других задач эффективным решением является диаграмма изгибающего момента.
Метод качественного структурного анализа занимает много времени и требует много практики, чтобы использовать его правильно и избежать путаницы.
Условия структурного поведения в качественном структурном анализе
Существует ряд определенных структурных моделей поведения, от которых зависит проведение качественного структурного анализа, и некоторые из них ясны и очевидны, в то время как другие могут быть не такими:
1. Типы опор и их ограничения: полностью закрепленная опора обеспечивает две реакции и один момент, защемленная опора имеет две реакции, а роликовая опора обеспечивает одну реакцию, которая является вертикальной, как показано в таблице 1. Таблица 1:
Таблица 1 Типы опор и их реакции
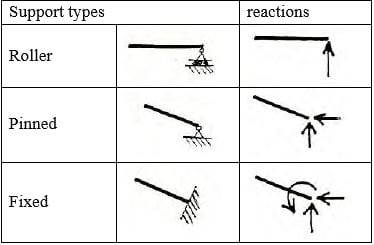
2. Момент на шарнире равен нулю.
3. Помните: момент равен силе, умноженной на расстояние.
4. Постройте диаграмму изгибающих моментов на стороне растяжения балки, чтобы сохранить последовательность ответов.
5. Для всех случаев нагружения конструкция остается в упругом диапазоне поведения материала. Напряжение пропорционально деформации, а прогибы прямо пропорциональны нагрузкам (первое предположение упругого анализа конструкций).
6. Прогибы, возникающие в результате нагружения, не приводят к развитию вторичных изгибающих моментов. Как показано в none; padding-top: 0px; padding-left: 0px; display: inline; padding-right: 0px; border: 0px;” title=”Качественный структурный анализ” src=”https://centrselstroy.ru/wp-content/uploads/2016/10/clip_image002.jpg” alt=”Качественный структурный анализ” width=”34″ height=”15″ border=”0″>. Вторичный момент ![]() пренебрегается. (Второе предположение упругого анализа конструкций).
пренебрегается. (Второе предположение упругого анализа конструкций).
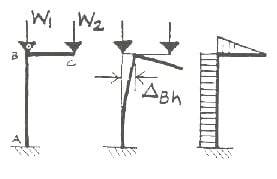
Консольный элемент ABC с нагрузками, прогибом и диаграммой изгибающего момента
7. В качественном анализе при определении изгибающего момента пренебрегают осевыми нагрузками в элементах, которые создают осевые деформации.
8. Принцип суперпозиции, который помогает упростить сложную конструкцию и рассматривать нагрузки по-разному, считается применимым при условии, что конструкция остается в упругом диапазоне.
Например: Двухпролетная балка ABC показана на рисунке Рисунок 2 с деформированной формой, реакциями и диаграммой изгибающих моментов. Используя принцип суперпозиции, неопределимая балка может быть легко решена.
Во-первых, удалите опору C, что приведет к просто опорной и консольной балке, затем постройте эпюру изгибающих моментов, как показано в левой части рисунка 3. Рисунок 3 Во-вторых, приложите силу Vc к C и постройте BMD, как показано в правой части рисунка 3. Рисунок 3.
Эти две диаграммы дают решение для исходной двухпролетной балки. Аналогичным образом можно рассматривать и прогибы.
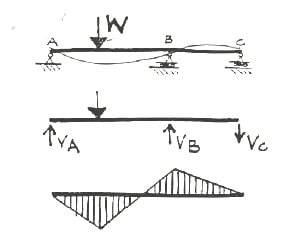
Рисунок 2 Балка ABC с отклоненной формой, реакциями и диаграммой изгибающего момента

Удалите реакцию в точке C (левая сторона), удалите W и вспомните реакцию C правой стороны, решите оба варианта, чтобы получить исходное решение.
9. В той части конструкции, которая остается прямой после нагрузки, нет изгибающего момента, однако она может двигаться.
10. Графики изгибающих моментов будут прямыми линиями, если приложенные нагрузки были точечными.
11. Диаграммы изгибающих моментов будут изогнутыми, если приложенные нагрузки были распределенными.
12. В простых опорах изгибающий момент равен нулю.
13. Эпюры изгибающих моментов пересекают элементы в точках встречного изгиба.
14. Рама без подкосов не будет раскачиваться, если она симметрична и симметрично нагружена.
15. Качественный анализ проводится для видимых нагрузок, поэтому собственным весом пренебрегают.
16. За исключением шарниров, формы прогибаемых элементов чрезвычайно гладкие.
17. В рамах углы жестких соединений должны сохранять первоначальные углы после нагрузок, как показано на рисунке Рисунок 4.
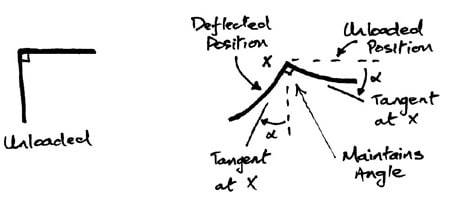
Угол жесткого шарнира рамы сохраняет прежний угол после нагрузки
18. В рамах жесткие шарниры могут закрываться или открываться, как показано на .
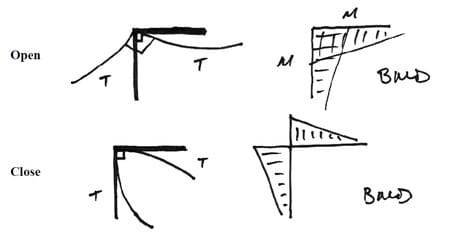
Раскрытие и закрытие жестких соединений после нагружения диаграммами изгибающих моментов
19. В жестких шарнирах, соединяющих два элемента, существует только одно значение момента.
20. Сдвигающая сила становится осевой силой, а осевая сила становится сдвигающей силой в переменных элементах при жестком соединении под прямым углом. Для проверки этого утверждения можно использовать sum(fx) = 0 , sum(fy) = 0. См. Рисунок 6
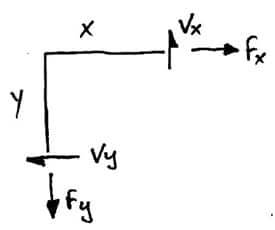
Жесткое соединение под прямым углом, при котором поперечная сила становится осевой, а осевая сила становится поперечной силой в переменном члене.
Однако это не так в соединении под косым углом, как показано на рисунке 7. Рисунок 7

Косоугольное соединение
21. В жестких соединениях, в которых имеется более двух членов, соединение должно находиться в равновесии. Как показано на рисунке Рисунок 8в следующем соединении MA = MB+MC
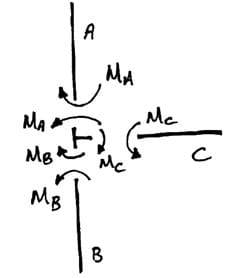
Равновесное жесткое соединение, в котором встречаются три элемента.
Полное решение качественного структурного анализа состоит из:
- Деформированная форма
- Реакции
- Диаграммы изгибающих моментов
Читайте далее:
- ТИПИЧНЫЕ СЛУЧАИ ОСЕВОЙ НАГРУЗКИ НА ЭЛЕМЕНТЫ КОНСТРУКЦИИ.
- Анализ рамы с сопротивлением моменту и распределение боковой нагрузки.
- Методы управления проектами – PERT, CPM и диаграмма Ганта.
- Метод распределения моментов в структурном анализе.
- Концепция проектирования высотных зданий из железобетона.
- Характеристики балок для их анализа и проектирования.
- Анализ фермы с примерами.