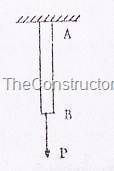
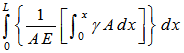ТИПИЧНЫЕ СЛУЧАИ ОСЕВОЙ НАГРУЗКИ НА ЭЛЕМЕНТЫ КОНСТРУКЦИИ - Строительство и ремонт

Проволока на рисунке 1 тянется под действием массы, прикрепленной к ее нижнему концу. В этом состоянии проволока находится в напряженном состоянии. Предположим, что общая нагрузка на поперечное сечение проволоки равна P, а площадь поперечного сечения проволоки равна A, тогда равномерное растягивающее напряжение () в проволоке равно ) в проволоке равно . Это называется интенсивностью силы P на площади поперечного сечения A.

0px; display: inline; border-top-width: 0px; border-bottom-width: 0px; border-left-width: 0px» title=»clip_image005″ border=»0″ alt=»clip_image005″ src=»https://centrselstroy.ru/wp-content/uploads/2010/09/clip_image00517.gif» width=»46″ height=»15″>или или или и т.д.

Когда силы P действуют на каждом конце бруса навстречу друг другу и если они стремятся сжать брус, то возникают сжимающие напряжения.

Растягивающие и сжимающие напряжения вместе называются прямые напряжения.

Практические ситуации, связанные с растягивающей силой:

a) Болт при затягивании подвергается растяжению.

b) Кабель, когда он провисает под собственным весом.

Практические ситуации сжимающих напряжений:

Колонна, несущая центральную осевую сжимающую силу.

ТИПИЧНЫЕ СЛУЧАИ ОСЕВОГО НАГРУЖЕНИЯ

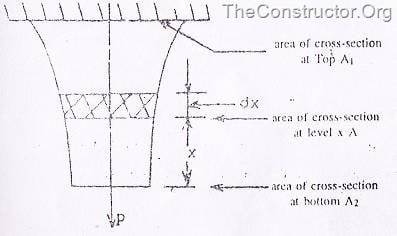
(a) Круглый сужающийся стержень, подверженный осевому растяжению (рисунок 2)

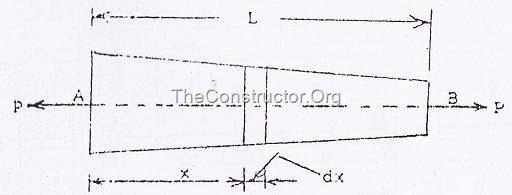
0px; display: inline; border-top-width: 0px; border-bottom-width: 0px; border-left-width: 0px» title=»clip_image010″ border=»0″ alt=»clip_image010″ src=»https://centrselstroy.ru/wp-content/uploads/2010/09/clip_image01015.gif» width=»21″ height=»22″> на одном конце и на другом конце длиной L, подвергается растягивающему усилию P.

Удлинение на небольшой длине

Где

Полное удлинение на длине AB =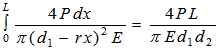

(b) Квадратный сужающийся брусок, подвергающийся осевому растяжению (рисунок 3)

Если брусок имеет длину L и квадратное сечение размером на одном конце и на одном конце и на другом конце общее удлинение составляет

(c) Прутки различного поперечного сечения, подвергающиеся осевому растяжению

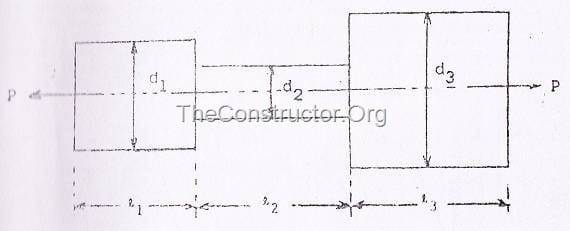
0px; display: block; float: none; border-top-width: 0px; border-bottom-width: 0px; margin-left: auto; border-left-width: 0px; margin-right: auto» title=»Бруски переменного сечения, подвергнутые осевому растяжению» border=»0″ alt=»Бруски переменного сечения, подвергнутые осевому растяжению» src=»https://centrselstroy.ru/wp-content/uploads/2010/09/clip_image0205.gif» width=»94″ height=»142″>.

Полное удлинение =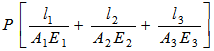

В общем случае полное удлинение определяется

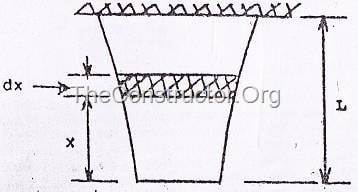
(d) Брусок одинаковой прочности

(рисунок 4)

Соотношение в изменении поперечного сечения, необходимого для обеспечения равномерной прочности по всей длине.

0px; display: inline; border-top-width: 0px; border-bottom-width: 0px; border-left-width: 0px» title=»clip_image001[2]» border=»0″ alt=»clip_image001[2]» src=»https://centrselstroy.ru/wp-content/uploads/2010/09/clip_image001211.gif» width=»19″ height=»13″>это напряжение в полосе в любом сечении, тогда из рассмотрения элементарной полосы dx,

где удельный вес полосы.

В пределе,

Интегрируя

или,

когда x = L,

(e) Удлинение бруса под собственным весом (рисунок 5)

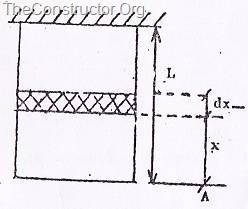
0px; display: inline; border-top-width: 0px; border-bottom-width: 0px; border-left-width: 0px» title=»clip_image034″ border=»0″ alt=»clip_image034″ src=»https://centrselstroy.ru/wp-content/uploads/2010/09/clip_image0342.gif» width=»53″ height=»41″>.

Где удельный вес бруса

общее удлинение бруса =

Если W — общий вес бруса, то общее удлинение =

Можно заметить, что общее удлинение, вызванное собственным весом бруса, равно удлинению, вызванному нагрузкой в половину его веса, приложенной к нижнему концу.

(f) Брусок различного сечения, подвергающийся растяжению под действием собственного веса (рис. 6)

0px; display: inline; border-top-width: 0px; border-bottom-width: 0px; border-left-width: 0px» title=»clip_image038″ border=»0″ alt=»clip_image038″ src=»https://centrselstroy.ru/wp-content/uploads/2010/09/clip_image0382.gif» width=»73″ height=»36″>.

Напряжения в полосе =

Удлинение в полосе =

Общее удлинение =

Читайте далее: