ОПТИМИЗАЦИЯ ТОПОЛОГИИ КОНСТРУКЦИЙ - Строительство и ремонт

ОПТИМИЗАЦИЯ ТОПОЛОГИИ КОНСТРУКЦИЙ С ИСПОЛЬЗОВАНИЕМ МЕТОД ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ

При разработке новых изделий очень важно найти наилучшую топологию или компоновку для заданных целей проектирования и ограничений на очень ранней стадии процесса проектирования (на стадии разработки концепции и определения проекта). Результат оптимизации топологии с использованием метода распределения материала представляет собой распределение плотности конечных элементов в области проектирования. Он все чаще используется, например, в автомобильной, машиностроительной и аэрокосмической промышленности, а также при проектировании материалов, механизмов и микроэлектромеханических систем (MEMS).

1. ВВЕДЕНИЕ

Все больше и больше человек осознает необходимость экономии природных

ресурсов. Этот факт является основной мотивацией для исследования оптимальных конструкций.

Инженеры-строители также переняли эту тенденцию при проектировании новых или модификации существующих конструкций. В этом контексте конструкцию можно рассматривать как количество распределенного материала в расчетной области, чтобы поддерживать нагрузки (статические или динамические), поглощать и распределять энергию и передавать ее на опоры. Одной из целей оптимального проектирования является наилучшее распределение имеющегося материала в расчетной области. Эта задача решается с помощью наиболее универсального вида структурной оптимизации, т.е. оптимизации топологии конструкции.

Оптимизацию топологии также называют оптимизацией компоновки или в общем смысле – оптимизацией формы. Оптимизация структурной топологии становится интересной областью исследований в сообществе структурной оптимизации. Важность этого типа оптимизации заключается в том, что выбор подходящей топологии структуры на концептуальной стадии, как правило, является наиболее решающим фактором для эффективности нового продукта.

2. Оптимизация топологии

Топология структуры определяется как пространственное расположение структурных элементов и соединений или внутренних границ. Следовательно, оптимизация топологии означает изменение связности между структурными элементами дискретных структур или между областями континуальных структур, как показано на рис. 1.1.

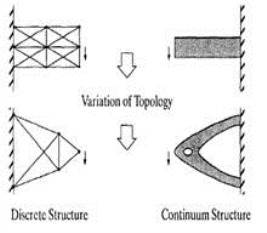
0px; border-left: 0px; display: inline; border-top: 0px; border-right: 0px” title=”” border=”0″ alt=”” src=”https://centrselstroy.ru/wp-content/uploads/2011/07/clip_image004.gif” width=”253″ height=”287″>.

–

2.11 Метод гомогенизации

2.12 Эволюционная структурная оптимизация (ESO)

2.13 Метод плотности и распределения

3. Структурная оптимизация

3.1 Основные понятия и определения

Структурная оптимизация направлена на систематическое повышение конструктивных характеристик компонентов и механических систем. Таким образом, сначала необходимо определить, какие переменные конструкции лучше всего описывают особенности какого-либо компонента. Затем, изменяя эти переменные в соответствии с некоторыми критериями, мы получаем наилучшее решение среди множества решений.

Проектные переменные для типичной задачи оптимизации конструкции могут быть размером элементов, конфигурацией конструкции, механическими или физическими свойствами материалов, или другими качественными аспектами для анализируемого проекта. Функция затрат, также известная как функция цели, – это скалярная функция, которая должна быть минимизирована (или максимизирована) в процессе оптимизации. Ограничения – это условия, накладываемые на физическую задачу, представляющие собой предел допустимого пространства.

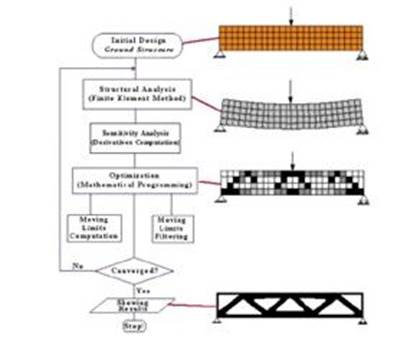
4. ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ

Результат оптимизации топологии с использованием распределения материалов представляет собой “распределение плотности” конечных элементов в расчетной области. Целевая функция заключается в минимизации податливости конструкции или максимизации жесткости конструкции. В литературе имеется много примеров, здесь приведены некоторые из них, основанные на минимальном соответствии.

Оптимизация топологии была выполнена с помощью стандартного кода оптимизации топологии Matlab.

Основная программа вызывается из интерпретатора Matlab строкой

top(nelx, nely, volfrac, penal, rmin)

где,

nelx и nely = количество элементов в горизонтальном и вертикальном направлениях, соответственно,

volfrac = объемная доля,

penal = мощность пенализации и

rmin = размер фильтра (деленный на размер элемента).

Другие переменные, а также граничные условия определены в самом коде Matlab и при необходимости могут быть отредактированы. Для каждой итерации в цикле оптимизации топологии код генерирует картину распределения плотности тока. Во всех примерах статических задач предполагается квадратный билинейный 4-узловой элемент.

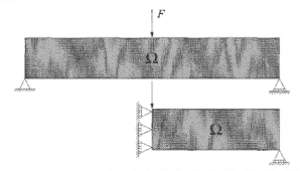
Пример: Просто подкрепленная балка.

Популярным примером минимальной податливости является балка MBB. Здесь – область проектирования, а F – единичная сила, приложенная к балке.

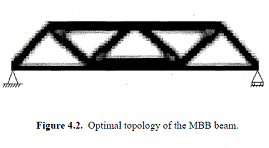
– Решение динамических задач при оптимизации топологии – далеко не тривиальное занятие. Численные проблемы, такие как

(i) локализованные собственные моды в областях с низкой плотностью, связанные с низким собственным значением; и

(ii) различные схемы интерполяции материала приводят к различным оптимальным топологиям.

– Эти проблемы не встречаются в статических задачах, хотя многие, если не все, задачи оптимизации топологии страдают от численных проблем, таких как шашечный метод, одноузловые связанные петли, зависимость от сетки и локальные минимумы.

– Проблема локализованных собственных мод успешно преодолевается с помощью схемы интерполяции материала.

– Критерий оптирнальности, по-видимому, более подвержен этой проблеме, и для ее решения требуется дальнейшая работа.

Читайте далее: