Существует ряд свойств балки, о которых инженер должен знать, поскольку они определяют поведение балки при воздействии нагрузки и в конечном итоге представляют собой возможные области или механизмы разрушения. Основными из них являются:
- Второй момент площади (также называемый вторым моментом инерции): зависит от профиля поперечного сечения балки и является мерой сопротивления формы балки изгибу.
- Изгибающий момент: обычно изображается на диаграмме изгибающего момента и часто связан с прогибом балки, может использоваться для расчета участков, подверженных максимальным изгибающим усилиям и, следовательно, наиболее вероятным изгибам. Она также показывает, какие участки балки находятся в состоянии сжатия или растяжения.
- Прогиб балки: прогиб балки, как правило, нежелателен и коррелирует с изгибающим моментом.
- Диаграммы сдвига: они используются для иллюстрации концентрации напряжений вдоль балки и позволяют определить области максимальных сдвигающих усилий, где балка с большей вероятностью разрушится от сдвига.
>Второй момент площади
Второй момент площади (I) – это свойство формы, используемое для прогнозирования сопротивления балки изгибу и прогибу.
Он рассчитывается на основе физической площади поперечного сечения балки и относится к массе профиля к нейтральной оси (это область, где балка не подвергается ни сжатию, ни растяжению, как обозначено на рисунке 5).
Он зависит от направления нагрузки; для большинства балок, за исключением полых и сплошных коробчатых и круглых сечений, второй момент площади будет отличаться при нагрузке в горизонтальном или вертикальном направлении.
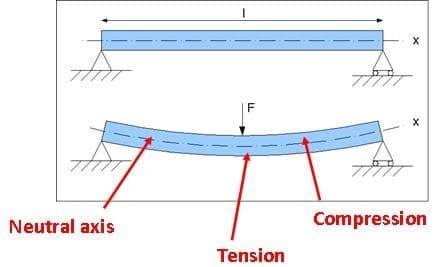
Рисунок 5 – a) просто подкрепленная балка длины l без силы; b) просто подкрепленная балка под действием точечной нагрузки (силы) F в центре, создающей изгиб.
Второй момент площади может быть рассчитан из первых принципов для любого профиля поперечного сечения с помощью уравнения:
![]()
Однако для распространенных профилей балок используются стандартные формулы:
I – балка / Универсальная балка
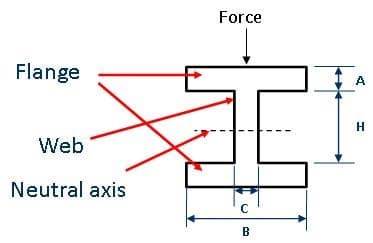
Рисунок 6 – Профиль поперечного сечения двутавровой балки с нагрузкой, параллельной полотну.
I – балка или универсальная балка имеет наиболее эффективный профиль поперечного сечения, так как большая часть материала расположена в стороне от нейтральной оси, обеспечивая высокий второй момент площади, что в свою очередь увеличивает жесткость, а значит, сопротивление изгибу и прогибу. Его можно рассчитать по формуле:
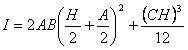
Как показано на рисунке 6, это подходит только для нагрузки параллельно полотну, так как нагрузка перпендикулярно полотну будет менее эффективной.
Коробчатое сечение
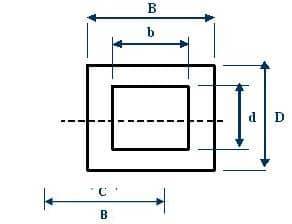
Рисунок 7 – Профиль поперечного сечения коробчатого сечения
Коробчатое сечение имеет наиболее эффективный профиль при горизонтальной и вертикальной нагрузке. Оно имеет меньшее значение второго момента площади, поэтому менее жесткое. Его можно рассчитать по формуле:
![]()
Диаграммы изгибающего момента и сдвига
Диаграммы изгибающего момента и сдвига обычно строятся вместе с диаграммой профиля балки, как показано ниже. Это позволяет точно представить поведение балки.
a) Представлена балка, на которую действует равномерно распределенная нагрузка (udl) величиной w по всей длине l. Общая сила на балке равна wl.
Балка просто поддерживается силами реакции R.
Расстояние x обозначает любую точку вдоль балки.
b) Диаграмма сдвигающих сил показывает области максимального сдвига, для данной балки они соотносятся с силами реакции.
Наклон диаграммы сдвигающих сил равен величине распределенной нагрузки.
Положительная сдвигающая сила заставит балку вращаться по часовой стрелке, а отрицательная сдвигающая сила заставит балку вращаться против часовой стрелки.
c) Максимальный изгибающий момент возникает, когда на балку не действуют поперечные силы.
Поскольку балка просто поддерживается, то есть подвержена только вертикальным силам реакции, изгибающий момент в этих точках не возникает. Если бы балка была ограничена, как в случае с консолью, то изгибающие моменты возникали бы на обоих концах В соответствии с диаграммами нагружения балки, максимальные значения поперечной силы и изгибающих моментов на расстоянии x вдоль балки можно рассчитать по следующей формуле:
Сила реакции и максимальная сдвигающая сила и Сдвигающая сила на расстоянии x
![]()
Максимальный изгибающий момент и Изгибающий момент на расстоянии x
![]()
Максимальный прогиб и Прогиб на расстоянии x
![]()
Эти формулы специфичны для данной ситуации с балкой, то есть равномерно распределенной нагрузки с простыми опорами, как показано на рисунке. Для консольной балки или балки с различными степенями свободы на опорах (это относится к ограничениям в горизонтальном направлении, подвергающим балку поворотному моменту в этом месте) потребуются другие формулы.
Все формулы могут быть рассчитаны на основе первых принципов, но для удобства можно использовать таблицы, подобные тем, которые содержатся в “Формулах Рорка для напряжения и деформации”.
Уравнения для максимального прогиба балки и прогиба на расстоянии x зависят от модуля Юнга, E и второго момента площади, I, в то время как поперечная сила и изгибающий момент не зависят от этих характеристик балки.
- Стальные гофрированные полотна в мостовых балках.
- Основы проектирования балок.
- Часовая башня Биг-Бен: тиканье с наклоном.
- Концепция проектирования высотных зданий из железобетона.
- Качественный структурный анализ балок и рам.
- Метод распределения моментов в структурном анализе.
- 21 Виды балок в строительстве [PDF].