Анализ рамы с сопротивлением моменту и распределение боковой нагрузки - Строительство и ремонт

Распределение боковой нагрузки каркасного здания

В двумерной раме с сопротивлением моменту каждый шарнир может иметь не более трех степеней свободы (смещение в горизонтальном и вертикальном направлениях и поворот).
Общее число степеней свободы равно 3Nj, где Nj – число шарниров в раме.
На практике балки несут очень маленькую осевую силу и испытывают незначительную осевую деформацию. Это означает, что горизонтальное смещение на всех шарнирах, расположенных на уровне балки, одинаково.
В большинстве зданий умеренной высоты осевая деформация колонн пренебрежимо мала.
Число степеней свободы сводится к одному повороту и одному горизонтальному смещению.
Поскольку вращательная инерция, связанная с вращательной степенью свободы, незначительна, то для проведения динамического анализа можно уменьшить количество степеней до одной на этаж путем статической конденсации.
Аналогичным образом, каждый шарнир трехмерной рамы может иметь не более шести степеней свободы.
Наконец, на каждый этаж приходится три степени свободы.
Таким образом, анализ свободной вибрации здания может быть проведен путем решения задачи (3N*3N) собственных значений, где N – количество этажей в здании.
После того, как известна собственная частота и форма, можно получить максимальную сейсмическую силу, которая должна быть приложена на каждом этаже при заданном движении грунта при землетрясении.

Анализ боковых нагрузок на раму, сопротивляющуюся воздействию моментов

После того, как известны расчетные боковые нагрузки на двумерные рамы, можно проанализировать раму на предмет сил, действующих на ее элементы.

Можно выполнить точный компьютерный анализ или приблизительный анализ в соответствии с требованиями.

Приблизительный анализ обычно выполняется на стадии предварительного проектирования и для оценки компьютерного анализа.

Два широко используемых метода:-

A. Метод портальной рамы:
Рамы: Портальные рамы часто используются над входом в мост и в качестве основного элемента жесткости в конструкции здания для передачи горизонтальных сил, приложенных в верхней части рамы, на фундамент. На мостах эти рамы противостоят силам, вызванным ветром, землетрясением и несбалансированной транспортной нагрузкой на мостовой настил. Порталы могут иметь штыревые опоры, неподвижные опоры или опоры с частичной фиксацией. Приблизительный анализ каждого случая будет рассмотрен для простого трехчленного портала.
Порталы со штыревой опорой: Типичная рама портала со штыревой опорой показана на рис. 1 (a). Поскольку на опорах существуют четыре неизвестных, но для решения доступны только три уравнения равновесия, эта конструкция является статически неопределимой в первой степени. Следовательно, необходимо сделать только одно допущение, чтобы свести раму к статически определимой.
Упругий прогиб портала показан на рис. 1(b). Эта диаграмма показывает, что точка перегиба, то есть место, где момент переходит от положительного изгиба к отрицательному, находится приблизительно в средней точке балки.
Поскольку в этой точке момент в балке равен нулю, мы можем предположить, что в этом месте существует шарнир, а затем определить реакции на опорах с помощью статики. Если это сделать, то окажется, что горизонтальные реакции (сдвиг) у основания каждой колонны равны, а остальные реакции соответствуют указанным на рис. 1(c). Кроме того, диаграммы моментов для этой рамы показаны на рис. 1(d).

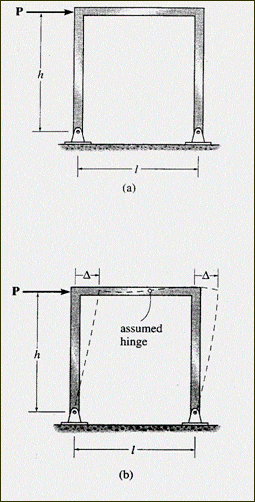
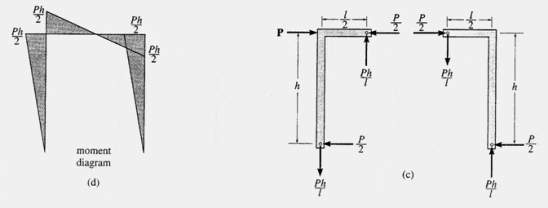
Рис. 1 Рама портала, закрепленная на основании с помощью штифтов

Порталы с неподвижными опорами: Портал с двумя неподвижными опорами, рис. 2(a), статически неопределим в третьей степени, поскольку на опорах имеется шесть неизвестных. Если вертикальные элементы имеют равные длины и площади поперечного сечения, то рама будет прогибаться, как показано на рис. 2(b).
Для этого случая мы будем считать, что точки перегиба находятся в средних точках всех трех элементов, и поэтому в этих точках расположены шарниры. Поэтому диаграммы реакций и моментов для каждого элемента можно определить, расчленив раму на шарниры и применив уравнения равновесия к каждой из четырех частей. Результаты показаны на рис. 2(c).
Обратите внимание, что, как и в случае портала со штыревым соединением, горизонтальные реакции (сдвиг) у основания каждой колонны равны. Диаграмма моментов для этой рамы показана на рис. 2(d).

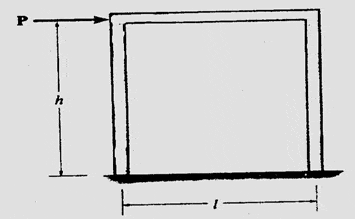
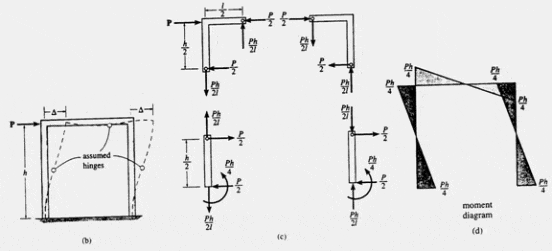
Рис. 2 Анализ портальных рам – Закрепленные в основании

Частично фиксированный (снизу) портал: Поскольку построить идеально неподвижную опору или фундамент для портальной рамы сложно и дорого, консервативной и в некоторой степени реалистичной оценкой является предположение о небольшом повороте в опорах, как показано на рис. 3(a). В результате точки перегиба на колоннах находятся где-то между случаем портала со штыревой опорой (как показано на рис. 1(a)), где “точки перегиба” находятся на опорах (основания колонн), и случаем портала с фиксированной опорой (как показано на рис. 2(a)), где точки перегиба находятся в центре колонн. Многие инженеры произвольно определяют местоположение на h/3 (рис. 3(b)), и поэтому размещают шарниры в этих точках, а также в центре балки.

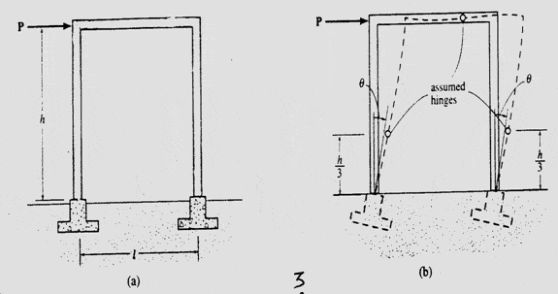
Рис. 3 Портальная рама, частично закрепленная в основании

Ферменные рамы: Когда портал используется для преодоления больших расстояний, вместо горизонтальной балки может быть использована ферма. Такая конструкция используется на больших мостах и в качестве поперечных прогибов для больших зрительных залов и мельничных зданий. Типичный пример показан на рис. 4(a).
Во всех случаях предполагается, что подвесная ферма имеет штыревое соединение в точках крепления к колоннам.
Более того, ферма удерживает колонны прямолинейными в области крепления, когда порталы подвергаются боковому воздействию D, рис. 4(b). Следовательно, мы можем анализировать ферменные порталы, используя те же допущения, что и для простых портальных рам.
Для колонн, опирающихся на штыри, предположим, что горизонтальные реакции (сдвиг) равны, как на рис. 1(c). Для колонн с фиксированной опорой предположим, что горизонтальные реакции равны и на каждой колонне имеется точка перегиба (или шарнир), измеряемая посередине между основанием колонны и самой низкой точкой соединения элементов фермы с колонной. См. рис. 2(c) и рис. 4(b).

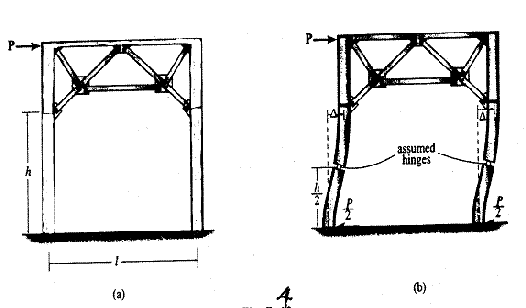
Рис. 4 Ферменная рама, закрепленная в основании

Боковые нагрузки на каркасы зданий: Метод портальной рамы

Действие боковых нагрузок на портальные рамы и установлено, что для рамы, закрепленной в основании, точки перегиба находятся приблизительно в центре каждой балки и колонны, а колонны несут равные сдвиговые нагрузки, рис. 2.
Изгиб здания прогибается так же, как и портальная рама, рис.5 (a), и поэтому уместно предположить, что точки перегиба находятся в центре колонн и балок.
Если считать, что каждый изгиб рамы состоит из ряда порталов, рис. 5 (b), то в качестве дополнительного допущения внутренние колонны будут представлять собой эффект двух портальных колонн и, следовательно, будут нести вдвое большую нагрузку на сдвиг V, чем две внешние колонны.
Рассмотрим двумерную раму с m-основанием и n-этажами. Степень неопределенности каркаса равна 3mn. Для анализа рамы необходимо сделать 3mn предположений;

Точка противодействия изгибу в колонне находится на середине высоты колонн: (m+1)n допущений.

Точка противоположного изгиба в балках находится на середине пролета балок: mn допущений.

Осевая сила во внутренних колоннах равна нулю (m+1)n допущений.

При вышеуказанных допущениях рама становится статически определимой, и силы в элементах получаются простым рассмотрением равновесия.

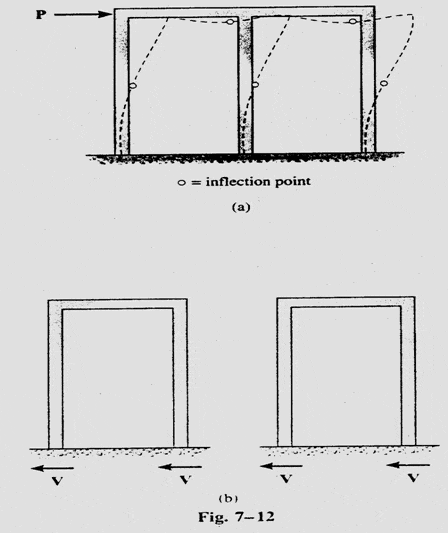
B. Консольный метод: В этом методе также необходимо сделать 3mn допущений, чтобы сделать раму статически определимой; точка противоположного изгиба в колонне находится на середине высоты колонн: (m+1)n допущений.

Точка противоположного изгиба в балках находится на середине пролета балок: mn допущений.

Осевая сила в колоннах аппроксимируется предположением, что рама ведет себя как консольная балка. Нейтральную ось рамы получают, используя площадь поперечного сечения колонны и местоположение колонны, осевое напряжение в колонне предполагается линейно изменяющимся от этой нейтральной оси: (m-1)n допущений.

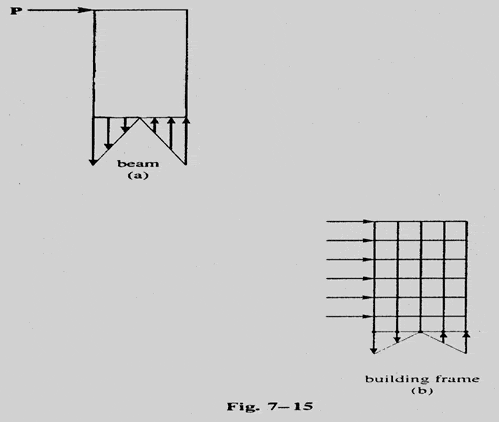
Консольный метод основан на том же действии, что и длинная консольная балка, подверженная поперечной нагрузке. Из механики материалов можно вспомнить, что такая нагрузка вызывает изгибающее напряжение в балке, которое линейно изменяется от нейтральной оси балки, рис. 6 (a).
Аналогичным образом, боковые нагрузки на раму стремятся опрокинуть ее или вызвать поворот рамы вокруг “нейтральной оси”, лежащей в горизонтальной плоскости, которая проходит через колонны на каждом уровне этажа. Чтобы противодействовать этому опрокидыванию, осевые силы (или напряжения) в колоннах будут растягивающими по одну сторону от нейтральной оси и сжимающими по другую сторону, как показано на рис. ниже.
Как и в случае с консольной балкой, представляется разумным предположить, что осевое напряжение имеет линейное изменение от центроида площади колонн или нейтральной оси. Поэтому консольный метод подходит для высоких и тонких рам или колонн с разной площадью поперечного сечения.

Читайте далее: