Арка определяется как плоскоизогнутый брус или ребро, поддерживаемое и нагружаемое таким образом, что оно действует на прямое сжатие. Арка является одним из старейших и долговечных структурных элементов традиционной архитектуры и предназначена для восприятия преимущественно вертикальных нагрузок. В строительной практике существует три основных типа арок: трехшарнирные, двухшарнирные и бесшарнирные.
Двухшарнирные и бесшарнирные арки представляют собой статически неопределимые конструкции, которые, как правило, более экономичны, жестки и прочны. Первая является неопределимой в первой степени, а вторая – в третьей. Бесшарнирная арка является очень эффективным элементом, но не подходит для легких применений, таких как трансформируемые конструкции.
- Анализ бесшарнирных арок
1. Две шарнирные арки
В двухшарнирных арках опоры позволяют поворачивать арку на концах под воздействием нагрузок, температурных колебаний и горизонтальных оседаний опор. Это делает арку относительно гибкой и менее склонной к развитию высоких изгибающих напряжений. Двухшарнирные арки являются статически неопределимыми первой степени с четырьмя силами реакции и тремя уравнениями равновесия.
Анализ двух шарнирных арок
Поскольку две шарнирные арки являются статически неопределимыми в первой степени, необходимо разработать еще одно уравнение для расчета всех реакций и построения диаграммы сдвига и изгибающего момента.
Четвертое уравнение составляется с учетом деформации арки. Неизвестная избыточная реакция Hb вычисляется, если учесть, что горизонтальное смещение шарнира B равно нулю.
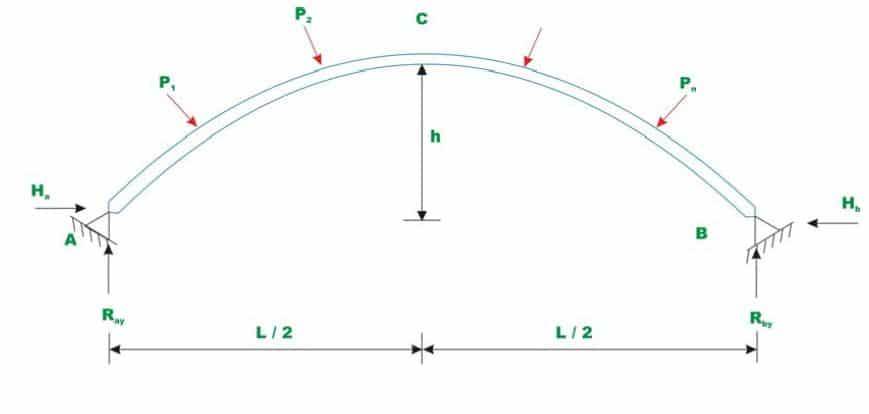 Реакции двух шарнирных арок
Реакции двух шарнирных арок
Hb вычисляется с помощью теоремы наименьшего произведения, которая гласит, что частная производная энергии деформации статически неопределимой конструкции по отношению к статически неопределимому воздействию должна исчезнуть. Общая форма уравнения, используемого для оценки Hb, выглядит следующим образом:
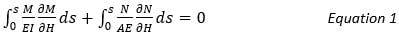
где:
s: Длина осевой дуги
M:
Изгибающий момент
E: модуль Юнга
модуль Юнга материала арки
I: Момент инерции поперечного сечения арки,
H: Горизонтальная реакция
N:
Осевое сжатие
A: Площадь поперечного сечения в любой координате
2. Бесшарнирные арки
В бесшарнирных арках, также известных как арки с фиксированным концом, опоры не допускают какого-либо поворота, поэтому относительный поворот или оседание на опоре создает значительные дополнительные напряжения.
Бесшарнирные арки статически неопределимы в третьей степени с тремя реакциями и тремя уравнениями равновесия. Двухшарнирные арки используются в обычных приложениях и не подходят для легких приложений.
Анализ бесшарнирных арок
Этот тип
является статически неопределимым с третьей степенью. Следовательно, необходимо разработать еще три
уравнений для расчета реакций и построения диаграмм сдвигов и моментов.
диаграммы сдвигов и моментов.
Существует ряд методов, с помощью которых можно анализировать арки с фиксированным концом, например: метод наименьшей энергии, метод аналогии колонн и метод упругого центра. Метод наименьшей энергии, который рассматривается здесь, используется для симметричных арок с симметричной нагрузкой.
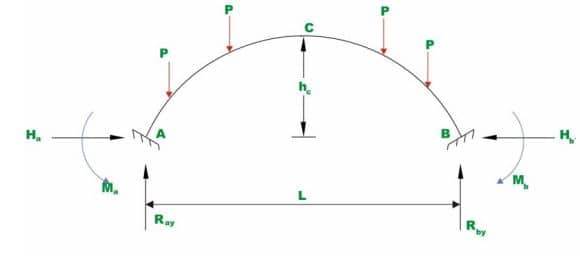 Реакция арки с фиксированным концом
Реакция арки с фиксированным концом
Для несимметричных арок с несимметричной нагрузкой можно использовать метод наименьшей энергии, но это требует дополнительных усилий. В этом случае может быть использована аналогия колонн или метод упругого центра.
Неизвестные реакции могут быть найдены с помощью формулы энергии деформации. Учитывая только энергию деформации при осевом сжатии и изгибе, энергия деформации U выражается как:
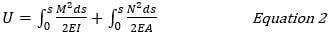
где,
M: Изгибающий момент
N: осевая сила ребра арки.
Поскольку опора в точке A на рис.2 неподвижна, уравнения для момента, сдвига и осевой силы в этой точке могут быть записаны следующим образом:
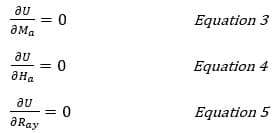
Поскольку размеры арки и нагрузки известны, неизвестные избыточные реакции Ma, Ha, Ray могут быть оценены с помощью вышеприведенных трех уравнений.
Поскольку арка и нагрузка симметричны, сдвигающая сила на венце равна нулю. Следовательно, на венце будет только две неизвестные силы. Следовательно, если внутренние силы на венце принять за избыточные, то выражение упрощается до:
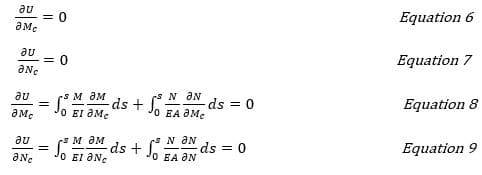
s: Длина осевой линии арки
I: Момент инерции поперечного сечения
A: Площадь поперечного сечения арки
Если Мо и Но – изгибающий момент и осевая сила в любом сечении под действием внешней нагрузки, то изгибающий момент и осевая сила в любом сечении задаются уравнениями:
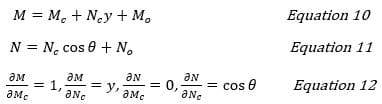
Уравнения 8 и 9 могут быть упрощены с помощью уравнений 10, 11 и 12.
Читайте далее:- Типы арочных конструкций по форме, материалу изготовления, качеству исполнения.
- Детерминированные и неопределенные структуры и их различия.
- Как выполнять кирпичную кладку в круглых и плоских арках? [PDF].
- Что такое арка? Различные компоненты арки.
- Метод распределения моментов в структурном анализе.
- Типы опор и реакций и их применение в конструкциях.
- Качественный структурный анализ балок и рам.