Центр сдвига – это точка на сечении балки, где приложение нагрузки не вызывает ее скручивания. Положение центра сдвига зависит от поперечного сечения балки. Например, центр сдвига и центр тяжести совпадают в симметричном сечении, но могут не совпадать с центроидом в случае несимметричного сечения.
Поэтому в несимметричных сечениях внешние силы должны проходить через центр сдвига, а не через центр тяжести сечения, иначе возникающий изгибающий момент будет сопровождаться кручением.
Как вычислить расположение центра сдвига?
Рассмотрим сечение швеллера, как показано на рис. 1. Теперь мы найдем положение плоскости, через которую вертикальные нагрузки должны действовать, чтобы вызвать простой изгиб, при этом ось x будет нейтральной осью.
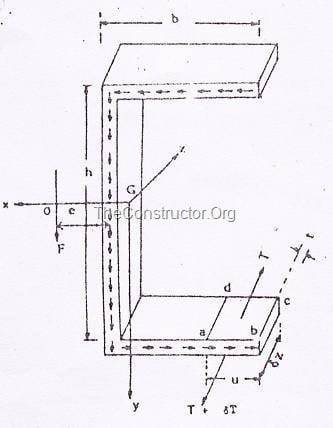 Сечение канала
Сечение канала
Можно предположить, что вертикальная срезающая сила F в сечении воспринимается только полотном. Во фланцах возникают горизонтальные напряжения сдвига, которые обозначаются как q.
Рассмотрим элемент ‘abcd‘, отрезанный от нижнего фланца двумя соседними сечениями (дельта z) друг от друга, и вертикальной плоскостью, параллельной полотну и расположенной на расстоянии ‘u‘ (которое является переменным) от свободного конца нижнего фланца.
Разница в растягивающих усилиях T и T+Дельта z должна быть равна силе сдвига на стороне ‘ad‘ элемента. Предполагая равномерное распределение напряжения сдвига (поскольку толщина мала) по толщине, имеем:
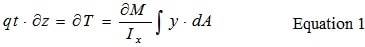
Интегрирование выполняется по части ‘ab’ фланца. Напряжение на единицу длины центральной линии сечения:
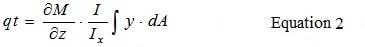
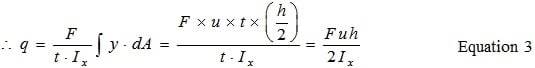
Таким образом, видно, что q пропорционально u. Максимальное значение q :

На стыке фланца и полотна распределение напряжения сдвига сложное, поэтому можно предположить, что уравнение 4 справедливо для u = 0 и u = b.
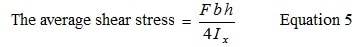


Предположим, что вертикальная сдвигающая сила F действует через точку ‘o‘, центр сдвига на расстоянии c от O на центральной линии полотна. Скручивания этого участка можно избежать, если:


что дает положение центра сдвига.
Примечание: Центр сдвига для сечений, имеющих одну ось симметрии, всегда расположен на оси симметрии. В случае двутавровой балки, симметричной относительно оси x и оси y, центр сдвига совпадает с центром сечения. Точное расположение центра сдвига для несимметричных сечений является сложным и может быть определено путем осмотра.
Пример:
Найдите центр сдвига несимметричного двутаврового сечения, как показано на рисунке ниже:
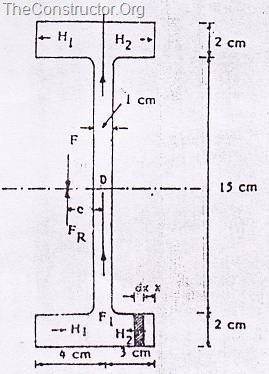
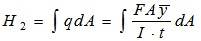
Здесь,
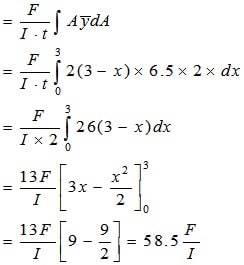
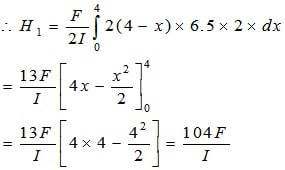
Возьмем момент относительно точки D:
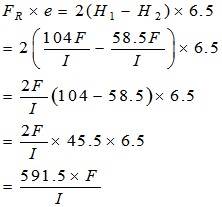
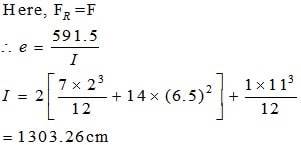
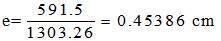
- Стальные гофрированные полотна в мостовых балках.
- Процедура проектирования железобетонной тавровой балки с примером.
- Как предотвратить скручивание бетона? [PDF].
- Концепция проектирования высотных зданий из железобетона.
- Анализ фермы с примерами.
- Что такое центр масс и центр тяжести?.
- Как спроектировать одностороннее перекрытие в соответствии с ACI 318-19? | Прилагается пример.