Кинематика потока в механике жидкости - уравнение разгрузки и неразрывности - Строительство и ремонт

В кинематике потока изучаются только параметры, вызывающие движение жидкости, а не силы, вызывающие движение частиц жидкости. Уравнение расхода и уравнение неразрывности – это темы, которые используются для изучения потока жидкости через трубу или канал.

Скорость потока или разряжение (Q)

Разряд или скорость потока (Q) определяется как количество жидкости, протекающей в секунду через канал или участок трубы. Эта скорость потока выражается в терминах “объем”, когда поток жидкости несжимаемый, и принимается в терминах “вес”, когда поток сжимаемый.

Для потока жидкости расход (Q) выражается в литрах/сек или м3/с, а для газообразного потока расход выражается в кгс/с или Ньютон/с.

Если жидкость, протекающая через трубу с площадью сечения “A”, имеет скорость “V”, то расход,

Q = A x V Eq.1

Уравнение непрерывности в механике жидкости

Уравнение неразрывности разработано на основе принципа сохранения массы. Уравнение неразрывности утверждает, что скорость потока жидкости через трубу постоянна во всех сечениях. То есть, количество жидкости в секунду постоянно по всему сечению трубы.

Рассмотрим жидкость, протекающую по трубе с различной площадью поперечного сечения, как показано на рисунке 1 ниже. Рассмотрим два сечения 1-1 и 2-2, как показано на рисунке.

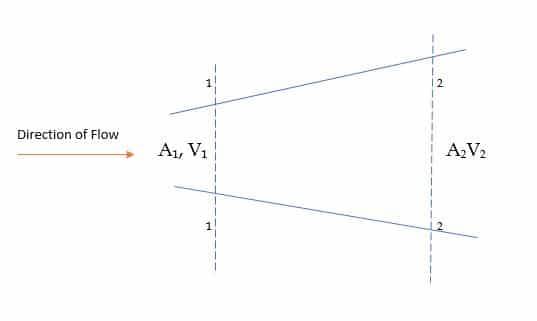Рис.1. Уравнение неразрывности в механике жидкости

Площадь сечения в секциях 1 и 2 равна A1 и A2 соответственно. Скорость и плотность жидкости в сечении 1-1 равны V1 и J1, а в сечении 2-2 – V2 и J2. Тогда, исходя из уравнения 1,

Скорость потока или расхода на участке 1-1 , Q1 = J1A1V1

Скорость потока или расхода на участке 2-2, Q2 = J2A2V2

Исходя из уравнения непрерывности, скорость потока жидкости в секции 1-1 равна скорости потока жидкости в секции 2-2. Тогда,

Q1 = Q2

J1A1V1 =J2A2V2

Приведенное выше уравнение применимо к сжимаемому потоку (поток жидкости, в котором плотность изменяется со временем). Для несжимаемого потока уравнение неразрывности задается уравнением,

A1V1 =A2V2

Уравнение неразрывности для 3D и 2D

Уравнение неразрывности для трехмерного и двумерного потока может быть выражено либо в декартовых координатах, либо в полярных координатах.

Уравнение неразрывности в декартовых координатах (3D)

Уравнение неразрывности в декартовых координатах может быть применимо для:

1. Стационарного и нестационарного течения жидкости

2. Равномерного и неоднородного течения жидкости

3. Сжимаемый и несжимаемый поток жидкости

Уравнение неразрывности для установившегося потока

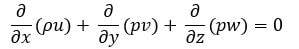
Уравнение неразрывности для несжимаемого потока

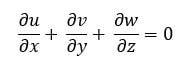
Уравнение неразрывности в декартовых координатах (2D)

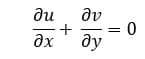
Уравнение непрерывности в полярных координатах

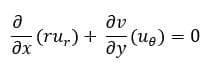
Читайте также: Что такое поток в открытом канале? Типы течения в открытых каналах

Читайте далее:

<\/div>window.yaContextCb.push(()=>{Ya.Context.AdvManager.render({\"blockId\": \"R-A-2348978-11\",\"renderTo\": \"yandex_rtb_R-A-2348978-11\"})})<\/scr"+"ipt>"; cachedBlocksArray[337936] = "

<\/div>window.yaContextCb.push(()=>{Ya.Context.AdvManager.render({\"blockId\": \"R-A-2348978-10\",\"renderTo\": \"yandex_rtb_R-A-2348978-10\"})})<\/scr"+"ipt>"; cachedBlocksArray[337935] = "

<\/div>window.yaContextCb.push(()=>{Ya.Context.AdvManager.render({\"blockId\": \"R-A-2348978-9\",\"renderTo\": \"yandex_rtb_R-A-2348978-9\"})})<\/scr"+"ipt>"; cachedBlocksArray[337934] = "

<\/div>window.yaContextCb.push(()=>{Ya.Context.AdvManager.render({\"blockId\": \"R-A-2348978-8\",\"renderTo\": \"yandex_rtb_R-A-2348978-8\"})})<\/scr"+"ipt>"; cachedBlocksArray[337933] = "

<\/div>window.yaContextCb.push(()=>{Ya.Context.AdvManager.render({\"blockId\": \"R-A-2348978-7\",\"renderTo\": \"yandex_rtb_R-A-2348978-7\"})})<\/scr"+"ipt>"; cachedBlocksArray[337932] = "

<\/div>window.yaContextCb.push(()=>{Ya.Context.AdvManager.render({\"blockId\": \"R-A-2348978-6\",\"renderTo\": \"yandex_rtb_R-A-2348978-6\"})})<\/scr"+"ipt>"; cachedBlocksArray[337931] = "

<\/div>window.yaContextCb.push(()=>{Ya.Context.AdvManager.render({\"blockId\": \"R-A-2348978-5\",\"renderTo\": \"yandex_rtb_R-A-2348978-5\"})})<\/scr"+"ipt>"; cachedBlocksArray[337930] = "

<\/div>window.yaContextCb.push(()=>{Ya.Context.AdvManager.render({\"blockId\": \"R-A-2348978-4\",\"renderTo\": \"yandex_rtb_R-A-2348978-4\"})})<\/scr"+"ipt>"; cachedBlocksArray[337940] = "

<\/div>window.yaContextCb.push(()=>{Ya.Context.AdvManager.render({\"blockId\": \"R-A-2348978-3\",\"renderTo\": \"yandex_rtb_R-A-2348978-3\",\"type\": \"feed\"})})<\/scr"+"ipt>"; -->