Изобара напряжения или концепция луковицы давления
Изобара или луковица давления – это контур напряжения или линия, соединяющая все точки под поверхностью земли, в которых вертикальное давление одинаково.
По сути, изобара представляет собой пространственную изогнутую поверхность и по форме напоминает луковицу; это происходит потому, что вертикальное давление во всех точках горизонтальной плоскости на равных радиальных расстояниях от нагрузки одинаково.
Таким образом, изобара напряжения также называется “луковицей давления” или просто “луковицей давления”. Вертикальное давление в каждой точке луковицы давления одинаково.
Давление в точках внутри колбы больше, чем давление в точке на поверхности колбы; а давление в точках вне колбы меньше этого значения.
Для любой приложенной нагрузки можно нарисовать любое количество луковиц давления, поскольку каждая из них соответствует произвольно выбранному значению напряжения.
Система изобар показывает уменьшение интенсивности напряжения от внутренних к внешним и напоминает “луковицу лука”. Отсюда термин “луковица давления”. Диаграмма изобар, состоящая из системы изобар, выглядит примерно так, как показано на рис. 1 и рис. 2.
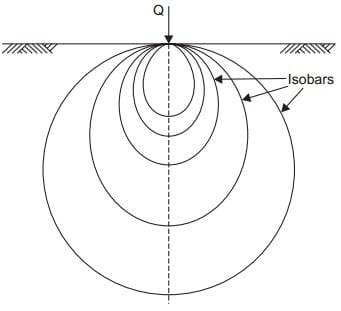
Изобара давления для точечных нагрузок
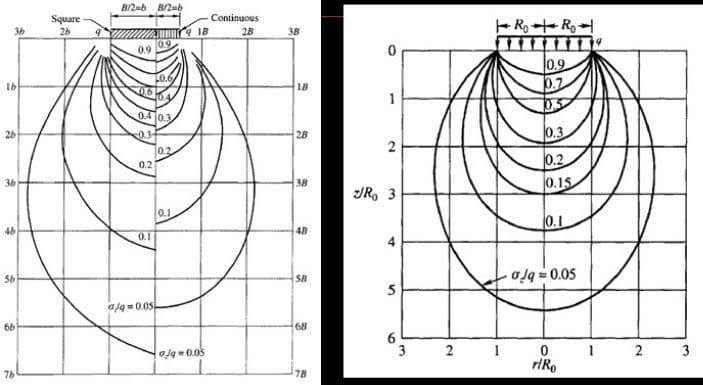
Изобара давления для основания
Порядок построения диаграммы изобар давления
Процедура построения изобары выглядит следующим образом:
1. Пусть требуется построить изобару, для которой 
на единицу площади (10% изобары).
Распределение напряжений дается по формуле:
, где,
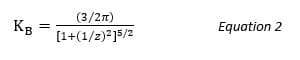
Таким образом,
2. Предполагая различные значения для z, вычисляются соответствующие KB-значения.
3. Для вычисленных значений KB получаются соответствующие r/z-значения.
4. Для предполагаемых значений z можно рассчитать r-значения.
Очевидно, что для одного и того же значения r на любой стороне оси z, или линии действия точечной нагрузки, величина 
одинаковы; следовательно, изобара симметрична относительно этой оси. Таким образом, вторая половина может быть получена из симметрии.
При r = 0, KB = 0,4775; изобара пересекает линию действия нагрузки на глубине:
Расчеты лучше всего проводить в виде таблицы, приведенной ниже:
Таблица 1: Данные для изобарына единицу площади.
Глубина z (единицы)
Коэффициенты влияния KB
r/z
r (единицы)
0.5
0.0250
1.501
0.750
0.1Q
1.0
0.1000
0.932
1.5
0.2550
0.593
0.890
2.0
0.4000
0.271
0.542
2.185
0.4775
0
0.1Q
- Что такое контурная съемка? Методы, карты и использование контуров в геодезии.
- Методы управления проектами – PERT, CPM и диаграмма Ганта.
- Определение удельного веса цемента и его значение.
- Стадион Нарендры Моди: Особенности строительства самого большого крикетного стадиона в мире.
- Диаграмма Ганта в управлении строительством – особенности и преимущества [PDF].
- Контурные линии и их типы, характеристики и использование в геодезии.
- Разница между PERT и Amp; диаграммы Ганта в управлении проектами [PDF].