Теория простого изгиба

Когда балка подвергается воздействию системы нагрузок или пары сил, действующих в плоскости, проходящей через ось, то балка деформируется. Проще говоря, эта осевая деформация называется изгибом балки. Под действием поперечной силы и изгибающего момента балка подвергается деформации. Эти нормальные напряжения, возникающие при изгибе, называются напряжениями изгиба.

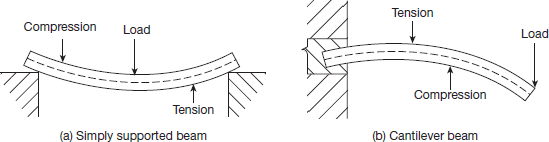
Виды напряжений изгиба в сечении балки

Допущения для расчета напряжений при изгибе

Напряжения, возникающие в материале при изгибе, могут быть рассчитаны с использованием определенных допущений, а именно

Виды напряжений при изгибе

1. Чистое напряжение изгиба

Изгиб называется чистым изгибом, когда он происходит исключительно из-за сцепления на его конце. В этом случае в балке не возникает напряжения сдвига. Но напряжение, которое будет распространяться в балке в результате этого, будет называться нормальным напряжением. Нормальное напряжение потому, что оно не вызывает никаких повреждений балки. Как показано ниже на рисунке.

ФИГ 2: Чистые напряжения изгиба – это напряжения, возникающие только из-за собственной нагрузки балки.

2. Напряжение простого изгиба

Изгиб называется простым изгибом, когда он возникает из-за самонагружения балки и внешней нагрузки. Этот тип изгиба также известен как обычный изгиб, и при этом типе изгиба в балке возникает как напряжение сдвига, так и нормальное напряжение. Как показано ниже на рисунке.

Напряжение при простом изгибе

Формула для напряжения при изгибе

Где,
M = изгибающий момент
I = момент инерции сечения относительно оси изгиба.
= напряжение в волокне на расстоянии ‘y’ от центроидальной/нейтральной оси.
E = модуль Юнга материала балки.
R = радиус кривизны изогнутой балки.
Если y заменить на c, расстояние до самого удаленного элемента, то


Где, Z = модуль упругости сечения и определяется, Z = I/c

Виды деформации при изгибе

1. Нормальные деформации

В результате изгиба где-то между верхней и нижней частями балки образуется поверхность, на которой продольные волокна не изменяют своей длины. Эта поверхность называется нейтральной поверхностью балки, а ее пересечение с любой плоскостью сечения – нейтральной осью сечения.
Все продольные волокна, кроме тех, которые находятся на нейтральной поверхности, либо удлиняются, либо укорачиваются, создавая тем самым продольные деформации .

Где k = кривизна = 1/R
Это уравнение показывает, что продольные деформации пропорциональны кривизне и линейно зависят от расстояния y от нейтральной поверхности. Это уравнение вытекает из геометрии деформированной балки и не зависит от свойств материала. Уравнение справедливо независимо от диаграммы напряжения-деформации материала.

2. Поперечная деформация

Осевые деформации сопровождаются боковыми или поперечными деформациями из-за влияния коэффициента Пуассона. Положительные деформации сопровождаются отрицательными поперечными деформациями .

где коэффициент Пуассона.
В результате этих деформаций форма поперечного сечения изменяется. Например, рассмотрим случай, когда балка прямоугольного сечения подвергается чистому изгибу так, чтобы вызвать растяжение в верхней части и сжатие в нижней.
Стороны прямоугольного сечения становятся наклонными друг к другу. Верхняя поверхность приобретает седлообразную форму. Если продольная кривизна в плоскости xy считается положительной, то поперечная кривизна в плоскости yz – отрицательной. Все плоскости балки, которые первоначально были параллельны нейтральной поверхности, развивают антипластическую кривизну.

Применимость формулы изгиба

Нормальные напряжения, определяемые по формуле изгиба, относятся к чистому изгибу, что означает отсутствие сдвигающих сил, действующих на поперечное сечение. В случае неравномерного изгиба наличие сдвигающих сил приводит к искривлению или деформации поперечного сечения, поэтому сечение, которое было плоским до изгиба, перестает быть плоским после изгиба.
Искривление вследствие сдвига значительно усложняет поведение балки, но более тщательный анализ показывает, что нормальные напряжения, рассчитанные по формуле изгиба, не претерпевают значительных изменений из-за наличия сдвиговых напряжений и связанного с ними искривления. Таким образом, использование теории чистого изгиба для расчета нормальных напряжений в случаях неравномерного изгиба считается оправданным.

• Армированный фибробетон – виды, свойства и преимущества армированного фибробетона.
• Концепция проектирования высотных зданий из железобетона.
• Теория анализа нагрузок Марстона-Спенглера для канализационной санитарной системы.
• Основы проектирования балок.
• Характеристики балок для их анализа и проектирования.
• ПРОЕКТИРОВАНИЕ СТАЛЬНЫХ КОМПРЕССИОННЫХ ЭЛЕМЕНТОВ.
• Режимы разрушения в бетонных балках: разрушение при изгибе и сдвиге.