Давление жидкости и закон Паскаля в механике жидкости

Давление жидкости и закон Паскаля кратко объясняются на примере небольшого элемента жидкости, находящегося в состоянии покоя. Концепция более подробно раскрывается на примере тренировки.

Давление жидкости в точке

Давление жидкости, действующее в точке, можно определить по формуле:

p =F/A;

Где F сила, действующая на жидкость на площади A.

Рассмотрим небольшую область dA в жидкости. Сила, действующая на область dA этой жидкости в состоянии покоя, направлена перпендикулярно поверхности dA. Если dF – сила, действующая перпендикулярно поверхности dA, то давление, действующее на точку в жидкости в состоянии покоя, определяется как,

p = dF/dA

Единицы измерения давления жидкости

Давление жидкости может быть измерено либо в единицах М.К.С, либо в единицах СИ. В единицах М.К.С давление измеряется в кгФ/см2 или кгФ/м2. В единицах S.I давление жидкости измеряется в Н/мм2 или Н/м2.

Примечание: 1Н/м2 = 1Па; 1бар Давление жидкости = 100кПа = 100000Па = 100000Н/м2

Что такое закон Паскаля?

Закон Паскаля гласит, что сила давления в точке статической жидкости одинакова во всех направлениях (x, y и z). Это доказывается следующим выводом.

Рис.1. Силы, действующие на элемент жидкости

Рассмотрим произвольный элемент жидкости ABC со сторонами AC, AB и BC как dx, dy и ds. Здесь ширина элемента принимается равной единице.

Пусть Px, Py и Pz – интенсивности давления, действующие на поверхности AB, AC и BC. Пусть угол ABC равен ‘Q’. Вся система жидкости показана на рисунке 1.

Силы, действующие на элемент жидкости, следующие:

1. Силы давления, действующие на элемент

Сила, действующая на AB = Px . Площадь грани AB = Px . dy . 1

Сила, действующая на AC = Py . Площадь грани AC = Px . dx . 1

Сила, действующая на BC = Pz . Площадь грани BC = Pz . ds . 1

2. Вес элемента жидкости

Вес элемента жидкости определяется следующим образом,

w = Масса элемента жидкости x g = ( Объем x плотность жидкости ) g

w = [( AB x AC)/2] . 1 . Плотность жидкости . g

Решив вопрос о силах в,

X-направлении

=> Px . dy.1 – Pz.ds.1.sin(90-Q) = 0;

=> Px . dy.1 – Pz.ds.cos Q = 0; [ Из рисунка-1, ds. cos(Q) = dy].

=> Px =Py; (Eq.2)

Y-направление

Py.dx.1 -Pz.ds.1.cos(90-Q) – [ (dx.dy)/2].1.density.g = 0

здесь также cos(90-Q) = sinQ и весом пренебрегаем, так как элемент очень мал. Отсюда получаем,

Py =Pz; (Eq.3)

Из уравнений 2 и 3 следует, что,

Px =Py=Pz

Приведенное выше уравнение утверждает, что давление в одной точке жидкости в состоянии покоя одинаково во всех направлениях.

Пример тренировки

Рассмотрим гидравлический пресс с плунжером диаметром 0,3 м и плунжером диаметром 4,5 см. Если сила, приложенная к плунжеру, равна 500 Н, определите вес, поднятый гидравлическим прессом.

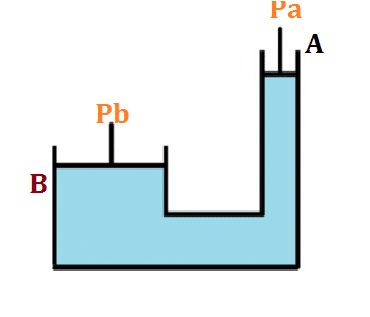Рис.2

Решение: Приведенные данные

Из рисунка 2 следует, что сила прикладывается к плунжеру, чтобы поднять груз W на другом конце гидравлического пресса. Система здесь подчиняется закону Паскаля. Согласно закону, напряжение, созданное в точке приложения силы (в точке A), равно напряжению, созданному в точке B. Тогда,

1. Напряжение в точке A = Pa = Сила / Площадь;

=> Pa = Сила / Площадь плунжера = 500/[(3.124 x .045 x .045)/4] = 314465.4N/m2

2. Интенсивность давления в точке B = Pb = Сила / Площадь плунжера;

=> Pb = Па (согласно закону Паскаля)

=> Pb = 314465,4 = Сила/площадь тарана;

Сила или поднятый вес = 314465,4 x Площадь тарана

= 314465,4 x [(3,14 x 0,3 x 0,3)/4]

Сила или поднятый вес = 22222 Н = 22,2 кН

Читайте также: Что такое напор в механике жидкости?

• СВОЙСТВА ЖИДКОСТИ.
• Различные виды давления в механике жидкости.
• Кинематика потока в механике жидкости – уравнение разгрузки и неразрывности.
• Что такое напор в механике жидкости?.
• Анализ фермы с примерами.
• Определение стандартной консистенции цемента.
• Технология гидравлических прицепов: Изменение размеров транспортной системы.