Что такое момент инерции?
Момент инерцииназываемый также моментом инерции массы или угловой массой, (единицы СИ кг м2) – это мера сопротивления объекта изменению скорости вращения. Это вращательный аналог массы. То есть, это инерция жесткого вращающегося тела по отношению к его вращению.
Момент инерции играет во вращательной динамике практически ту же роль, что и масса в основной динамике, определяя связь между угловым моментом и угловой скоростью, крутящим моментом и угловым ускорением, а также некоторыми другими величинами. Хотя для многих ситуаций достаточно простой скалярной обработки, более продвинутая тензорная обработка позволяет анализировать такие сложные системы, как вращающиеся вершины и движение гироскопа.
Для обозначения момента инерции обычно используется символ I и иногда J.
Момент инерции объекта относительно данной оси описывает, насколько трудно изменить его угловое движение относительно этой оси. Например, рассмотрим два диска (A и B) одинаковой массы. Диск А имеет больший радиус, чем диск В. Если предположить, что толщина и распределение массы равномерны, то для ускорения диска А (изменения его угловой скорости) требуется больше усилий, поскольку его масса распределена дальше от оси вращения: масса, находящаяся дальше от оси, должна для данной угловой скорости двигаться быстрее, чем масса, находящаяся ближе. В этом случае диск A имеет больший момент инерции, чем диск B.
Момент инерции имеет две формы: скалярную форму I (используется, когда известна ось вращения) и более общую тензорную форму, которая не требует знания оси вращения. Скалярная форма I (часто называемая просто “моментом инерции”) позволяет кратко проанализировать многие простые проблемы в динамике вращения, такие как скатывание объектов по наклонной плоскости и поведение шкивов.
Например, хотя блок любой формы будет скользить вниз по наклонной плоскости с одинаковой скоростью, катящиеся объекты могут спускаться с разной скоростью, в зависимости от их моментов инерции. Обруч будет спускаться медленнее, чем сплошной диск равной массы и радиуса, потому что большая часть его массы расположена далеко от оси вращения и, следовательно, должна двигаться быстрее, если обруч катится с той же угловой скоростью.
Однако для (более сложных) задач, в которых ось вращения может меняться, скалярный метод неадекватен, и необходимо использовать тензорный метод (хотя в особых ситуациях возможны сокращения). Примеры, требующие такого обращения, включают гироскопы, вершины и даже спутники – все объекты, чья центровка может меняться.
Момент инерции не следует путать с полярным моментом инерции, который является мерой способности объекта сопротивляться кручению (скручиванию).
Формула момента инерции:
Простая формула момента инерции любого объекта, будь то точечная масса или 3D-структура, дается следующим образом:
![]()
где
dm – масса бесконечно малой части тела
и r – (перпендикулярное) расстояние точечной массы до оси вращения.
Подробный анализ
(Скалярный) момент инерции точечной массы, вращающейся вокруг известной оси, определяется следующим образом
![]()
I является аддитивным. Таким образом, для твердого тела, состоящего из N точечных масс mi с расстояниями ri до оси вращения, общий I равен сумме моментов инерции точечных масс:
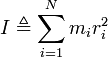
Для твердого тела, описываемого непрерывной функцией плотности массы ?(r), I вокруг известной оси может быть вычислена путем интегрирования квадрата расстояния (взвешенного по плотности массы) от точки тела до оси вращения:
![]()
V – объем, занимаемый объектом.
? – функция пространственной плотности объекта, и
![]() координаты точки внутри тела.
координаты точки внутри тела.
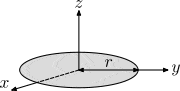
Диаграмма для расчета I диска. Здесь k – 1/2, а r – радиус, используемый при определении момента.
Исходя только из анализа размеров, I неточечного объекта должна иметь вид:
![]()
M – масса
R – радиус объекта от центра масс (в некоторых случаях вместо него используется длина объекта).
k – безразмерная постоянная, называемая константой инерции, которая изменяется в зависимости от рассматриваемого объекта.
Инерционные константы используются для учета различий в размещении массы от центра вращения. Примеры включают:
k = 1, тонкое кольцо или тонкостенный цилиндр вокруг своего центра,
k = 2/5, твердая сфера вокруг своего центра
k = 1/2, твердый цилиндр или диск вокруг своего центра.
Теорема о параллельных осях
После того как момент инерции вычислен для вращения вокруг центра масс твердого тела, его можно удобно пересчитать и для всех параллельных осей вращения, не прибегая к формальному определению. Если ось вращения смещена на расстояние R от оси центра масс (например, вращение диска вокруг точки на его периферии, а не через центр), то смещенный и центральный моменты инерции связаны следующим образом:
![]()
Эта теорема также известна как правило параллельных осей и является частным случаем теоремы Штейнера о параллельных осях.
Теорема о перпендикулярных осях
Теорему о перпендикулярных осях для плоских объектов можно продемонстрировать, рассмотрев вклад в трехосные моменты инерции от произвольного элемента массы. Из момента массы точки, вклады в каждый из осевых моментов инерции составляют

Составные тела
Если тело может быть разложено (физически или концептуально) на несколько составных частей, то момент инерции тела вокруг данной оси получается суммированием моментов инерции каждой составной части вокруг той же заданной оси.
Моменты инерции распространенных форм
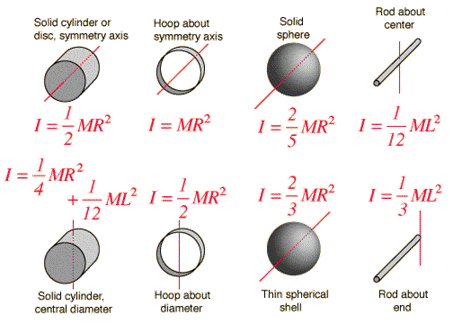
- Что такое центр масс и центр тяжести?.
- Что такое потенциальная функция скорости и функция потока?.
- Испытание маятника на кручение металлической проволоки.
- Испытание маятника на кручение металлической проволоки.
- Формулы Чези и Мэннинга в потоке в открытом канале.
- Что такое формула Чези для открытых каналов? Как определить постоянную Чези?.
- Метод распределения моментов в структурном анализе.